Electric field due to n charges

[member 731016]

Homework Statement

Please see below.

Relevant Equations

Please see below.

For this problem,

The solution is,

However, should they be a vertical component of the electric field for the expression circled in red? I do understand that assuming that when the nth charge is added it is placed equal distant for the other charges so that a component of the electric field cancels which would be the y-component from how they defined the coordinate system.

I also note how they could have just used the formula for the E-field produced by a discrete number of charges.

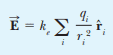
Many thanks!

 

[kuruman]

I assume that by "vertical" you mean a component in the plane parallel to the plane of the circle. Consider a point on the x-axis. If there were such a component of the field at that location, at what "o' clock" position relative to the circle would it point? To make it easy, assume that there are 12 charges on the circle labeled 1 - 12.

 

[member 731016]

I assume that by "vertical" you mean a component in the plane parallel to the plane of the circle. Consider a point on the x-axis.

Thanks for the reply @kuruman , and sorry for the late reply!

Yep, correct was what I meant by "vertical" :)

If there were such a component of the field at that location, at what "o' clock" position relative to the circle would it point? To make it easy, assume that there are 12 charges on the circle labeled 1 - 12.

If there was a positive charge on the x-axis, then I think there would be a electric field surrounding the charge. If there was a spherical Gaussian surface then then there would be a postive electric flux since there would only be electric field lines leaving the charge. But if there were charges on the circle, I think their vertical component will cancel from symmetry. I think the same is true for an even number of charges.

Is there a way to prove that the vertical component of the electric fields cancels from symmetry?

Many thanks!

 

[nasu]

If the unit vector $\hat{i}$ is supposed to mean the unit vector along the x axis the formula outlined in red is wrong. The field of any individual charge is not along the x axis but at an angle, as shown in the figure. This field does have a component perpendicular to the x axis. Only when you add all contributions the off-axis components cancel out.

 

[member 731016]

If the unit vector $\hat{i}$ is supposed to mean the unit vector along the x axis the formula outlined in red is wrong. The field of any individual charge is not along the x axis but at an angle, as shown in the figure. This field does have a component perpendicular to the x axis. Only when you add all contributions the off-axis components cancel out.

Thanks for you reply @nasu ! So really that formula shown in red for the individual charge n should be,

Correct?

However, how do we prove without using intuition that y-component of the radical fields cancel for n > 1 to give a resultant electric field of

for n charges?

I think the easiest situation to prove this for is for n = 2.
I'll assume that the two charges are separately symmetrically from each other by a distance 2a.

Then,

However, this does not give

mentioned in the solutions. Do you please know what I did wrong?

Thank you!

 

[kuruman]

Then,
View attachment 320343
However, this does not give View attachment 320344 mentioned in the solutions. Do you please know what I did wrong?

Thank you!

If you substitute $n=2$, it gives exactly that.

 

[member 731016]

If you substitute $n=2$, it gives exactly that.

Thanks @kuruman, I did not see that!