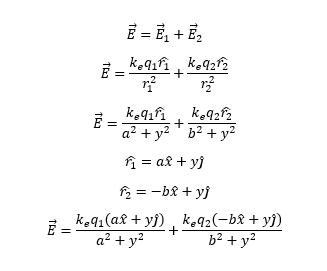Your expression is dimensionally incorrect. The spatial dependence goes as the inverse length not as the inverse length squared. As
@TSny noted, you need unit vectors.
If you have a point charge ##q## at position ##\mathbf{r'}##, the electric field vector at a point located at ##\mathbf{r}## is given by $$\mathbf{E}=\frac{k_e~ q(\mathbf{r}-\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|^3}.$$ To see how it works in this case, consider the negative charge ##q_2##.
Its position is ##~~\mathbf{r'}_2=b~\hat i##
The point of interest is at ##~~\mathbf{r}=y~\hat j##
Then
##\mathbf{r}-\mathbf{r'}_2=-b~\hat i+y~\hat j~;~~## ##|\mathbf{r}-\mathbf{r'}_2|=(b^2+y^2)^{1/2}##
With this mind, the electric field due to ##q_2## is $$\mathbf{E_2}=\frac{k_e ~q_2(-b~\hat i+y~\hat j)}{ \left(b^2+y^2\right)^{3/2}}.$$ Note that this expression is a magnitude $$E_2=\frac{k_e ~q_2}{ b^2+y^2}$$ multiplied by a unit vector $$\mathbf{\hat e}_2=\frac{(-b~\hat i+y~\hat j)}{ \left(b^2+y^2\right)^{1/2}}.$$Your expression was almost there.