Electric Field from a Charged Semicircular Rod

[ISAZI]

Homework Statement:

Help with Electric field homework

Relevant Equations:

E⃗ =
Q2ϵ0L2i^

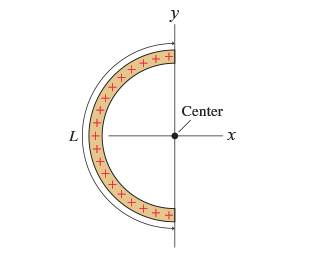
Charge QQ is uniformly distributed along a thin, flexible rod of length LL. The rod is then bent into the semicircle shown in the figure (Figure 1).


Find an expression for the electric field E⃗ E→ at the center of the semicircle.
Hint: A small piece of arc length ΔsΔs spans a small angle Δθ=ΔsΔθ=Δs /R/R, where RR is the radius.
Express your answer in terms of the variables QQQ, LLL, unit vectors i^i^i_unit, j^j^j_unit, and appropriate constants.

I really don't even know where to start here as there really isn't a lecture in this course.

I know that

electric field= q/r^2

so my first though was to rewrite R using arc length. Then I realized arc length won't really help. so I figured I had to write the formula in away that accounts for the radius at any given point or so I thought.

I know there's a really long formula1/4piepisolon * q/r^2 cos theta which could be written as xq/(x^2+d^2)^3/2. I know I have to think about the question carefully but I'm lost so I was wondering if somebody could help me understand better what it is that I'm trying to find and how I can think about the question and come to the conclusion. I already have the answer but its the path to the answer that I'm searching

 

[DaveE]

The force on a charge at the center will be the sum of all of the forces created by the charges on the semi-circle. You can break up the semi-circle into little arcs (Δs), calculate how much charge is in each piece and the direction it is pulling (Θ), then add them all up. You will then have an integral over Θ for the total force (field).

Hint: there are symmetries in the problem that may help simplify things.

 

[vela]

I really don't even know where to start here as there really isn't a lecture in this course.

Given what you wrote after this, I wouldn't say you don't have any idea where to start. Give yourself some credit!

You do have a textbook. It's a good resource and filled with tips on how to attack problems. Now I realize a lot of students don't like reading the textbook, but it's a skill you really need to practice and develop to succeed in college. Also, I think Knight is one of the more accessible physics textbooks. (Plus you probably paid a lot of money for the book. You might as well try to get you're money's worth.)

You can find problems worked out in the book. They might look like very different situations, but you should be able to see that there's a common pattern to how these kinds of problems are solved. It's that pattern that you need to learn.

I know that

electric field= q/r^2

Not quite. You forgot $k_e = 1/4\pi\epsilon_0$, and that expression only gives you the magnitude of the electric field, not the direction. The electric field is a vector field.

More important, the expression only applies to the electric field of a point charge. In electromagnetism, you're going get a bunch of formulas for $E$ and similar looking formulas for the potential. It's really important to understand what each formula is used for. I'd suggest making a summary sheet of the formulas so you have them on hand when doing your homework.

I know there's a really long formula1/4piepisolon * q/r^2 cos theta which could be written as xq/(x^2+d^2)^3/2. I know I have to think about the question carefully but I'm lost so I was wondering if somebody could help me understand better what it is that I'm trying to find and how I can think about the question and come to the conclusion. I already have the answer but its the path to the answer that I'm searching

You're jumping ahead here. Start with DaveE's suggestion and break the arc up into little pieces. Then consider the electric field at the origin due to just that one piece. Tell us what you get for that. Remember, both magnitude and direction.