- #1
Tapehead2
- 16
- 0
Electric Field from Arc of Charge - NEED HELP WITHIN AN HOUR
I have literally been working on this all day and I am finally turning it over to someone better at physics then myself. This is due within two hours and I'm starting to doubt my ability to finish this, any help will be beneficial. Thanks!
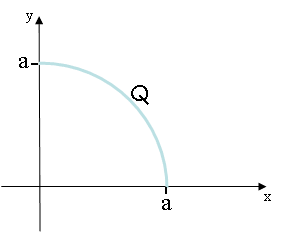
A total charge Q = -1.2 μC is distributed uniformly over a quarter circle arc of radius a = 6.1 cm as shown.
1) What is λ the linear charge density along the arc?
C/m
2) What is Ex, the value of the x-component of the electric field at the origin (x,y) = (0,0) ?
N/C
3) What is Ey, the value of the y-component of the electric field at the origin (x,y) = (0,0) ?
N/C
4)
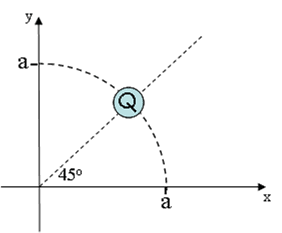
How does the magnitude of the electric field at the origin for the quarter-circle arc you have just calculated comnpare to the electric field at the origin produced by a point charge Q = -1.2 μC located a distance a = 6.1 cm from the origin along a 45o line as shown in the figure?
a. The magnitude of the field from the point charge is less than that from the quarter-arc of charge.
b. The magnitude of the field from the point charge is equal to that from the quarter-arc of charge
c. The magnitude of the field from the point charge is greater than that from the quarter-arc of charge
5)
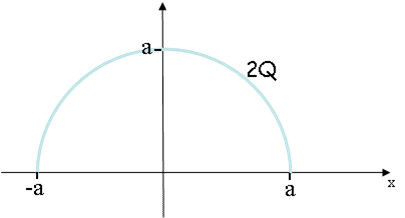
What is the magnitude of the electric field at the origin produced by a semi-circular arc of charge = -2.4 μC, twice the charge of the quarter-circle arc?
(2*pi*r)/4
(2*pi*.061m)/4=.0958m (the circumference of the circle we are concerned about)
(-1.2*10^-6)C/.0958m = -.000013 C/m
That is what I would say the density is but it is marked as incorrect. I cannot move on from this point. Any help will be great, thanks!
I have literally been working on this all day and I am finally turning it over to someone better at physics then myself. This is due within two hours and I'm starting to doubt my ability to finish this, any help will be beneficial. Thanks!
Homework Statement
A total charge Q = -1.2 μC is distributed uniformly over a quarter circle arc of radius a = 6.1 cm as shown.
1) What is λ the linear charge density along the arc?
C/m
2) What is Ex, the value of the x-component of the electric field at the origin (x,y) = (0,0) ?
N/C
3) What is Ey, the value of the y-component of the electric field at the origin (x,y) = (0,0) ?
N/C
4)
How does the magnitude of the electric field at the origin for the quarter-circle arc you have just calculated comnpare to the electric field at the origin produced by a point charge Q = -1.2 μC located a distance a = 6.1 cm from the origin along a 45o line as shown in the figure?
a. The magnitude of the field from the point charge is less than that from the quarter-arc of charge.
b. The magnitude of the field from the point charge is equal to that from the quarter-arc of charge
c. The magnitude of the field from the point charge is greater than that from the quarter-arc of charge
5)
What is the magnitude of the electric field at the origin produced by a semi-circular arc of charge = -2.4 μC, twice the charge of the quarter-circle arc?
The Attempt at a Solution
(2*pi*r)/4
(2*pi*.061m)/4=.0958m (the circumference of the circle we are concerned about)
(-1.2*10^-6)C/.0958m = -.000013 C/m
That is what I would say the density is but it is marked as incorrect. I cannot move on from this point. Any help will be great, thanks!
Last edited: