- #1
Philip KP
- 18
- 2
Homework Statement
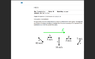
The figure below shows five protons that are launched in a uniform electric field E (green). The magnitude and direction of the launch velocities are indicated. Rank the protons according to the magnitude of their accelerations due to the field, greatest first. Justify.
https://canvas.ewu.edu/courses/1017106/files/35335813/preview
Homework Equations
E=k(Q/r^2)
–e = –1.60 * 10–19 C.
E=F/Q
F=k((Qxq)/(r^2))
F=ma
The Attempt at a Solution
Well I know that the charge of proton is the positive value of the charge of electron. I also feel like I know which equations are needed, but I'm not sure about if for instance proton d is moving at 5m/s after it is going against the electric field? That means the acceleration must be pretty great to go against the uniform electric field. I'm not sure, I feel lost and can't meet with teacher until after its due. Any help appreciated