Electric Field & Interplay between Coordinate Systems | DJ Griffiths

[warhammer]

Hi. I believe I have what may be both a silly and or a weird query. In many Griffiths Problems based on Electric Field I have seen that a coordinate system other than Cartesian is being used; then using Cartesian the symmetry of the problem is worked out to deduce that the field is in (say) z direction and then we specify everything else in Spherical/Polar/Cylindrical coordinates depending upon the dimensions and symmetry at hand to find the Electric Field in "z direction".

If what I have expressed above is not clear in words then I would like to point out Problems 2.6 & 2.7 whose statements are listed below along with part of my correct worked out solutions relevant to the query respectively.

2.6 : Find the electric field a distance z above the center of a flat circular
disk of radius R (Fig. 2.10) that carries a uniform surface charge σ. What does your
formula give in the limit R → ∞? Also check the case z >>R.

You can see in the below image that we take components (cosθ) along $\hat z$ while everything else including the integration is in Polar Coordinates. How/Why is this happening?

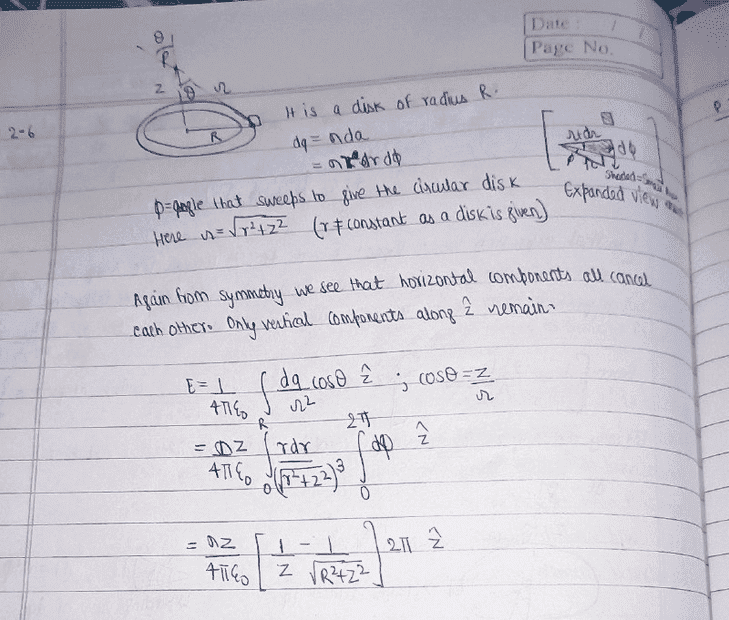
2.7: Find the electric field a distance z from the center of a spherical surface
of radius R (Fig. 2.11) that carries a uniform charge density σ. Treat the case z < R
(inside) as well as z > R (outside). Express your answers in terms of the total charge
q on the sphere.

Again in the below figure, components only along $\hat z$ prevail (characterised by cosα) while everything else is in terms of spherical coordinates.

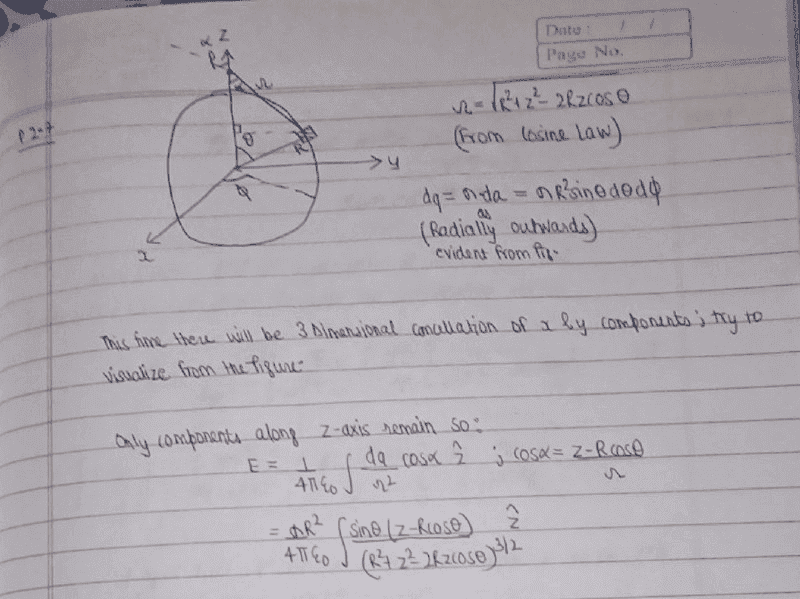
I am aware that the methods above are true but why are they true, in the sense that this seems like usage of 2 different coordinates systems mashed into one. So what is the cause behind this or what is the mistake in my reasoning above..

EDIT 1: $\hat r = (...) \hat x + (...) \hat y + cos\theta \hat z$ and $\hat z = cos\theta \hat r - (..) \hat theta$
Is the interplay between 2 coordinate systems used in P2.7 explained by the above relationships (given that we take the field to be emanating radially outward from vantage point of spherical coordinates?)

 

[vanhees71]

The great thing of vector calculus is that it deals with invariant quantities. Indeed the physics must not depend on the coordinates you arbitrarily choose to describe a problem. It's clear that a good choice in the beginning can tremendously simplify the solution. Particularly you should use the coordinates that are adapted to possibly present symmetries. That's why one works out also the generally covariant formalism, which works for any choice of generalized coordinates. In introductory textbooks you usually only consider the special case of curvilinear orthogonal coordinates, where the tangent vectors along the coordinate lines are all mutually orthogonal to each other, and then you also choose the normalized tangent vectors as the local basis vectors.

Nevertheless in the cases discussed above, it's more convenient to use Cartesian coordinates and just use parametrizations of the geometry of the charge distributions in terms of generalized coordinates (parameters).

The reason for Prob. 2.6 is that the author has restricted himself to the simplest special symmetrical case, i.e., the field along the symmetry axis of the disc. The general solution is much more complicated and involves even some elliptic functions I guess. Then you should rather work in cylindrical coordinates only.

For this special case, it even makes sense to blindly use the standard integral solution with the Green's function as given in your solution.

The reason for Prob. 2.7 is that you can restrict yourself to calculate the field along the $z$-axis, because everything is spherically symmetric, i.e., you get the general solution by calculating this special case, and then you know the solution everywhere due to symmetry.

Here, I'd however say, it's not good advice to use the integral. It's much easier to use the differential form in spherical coordinates. It's clear that the potential must be a function of $r$ only, and then with the Laplacian in spherical coordinates you simply have
$$\frac{1}{r} [r \Phi(r)]''=\rho/\epsilon_0.$$
For the spherical shell of radius $R$ with a homogeneous surface charge density, $\sigma$ you have
$$[r \Phi(r)]''=0$$
except at $r=R$, where you have to adjust the singularities of your solution to the given surface charge distribution. So except at $r=R$ the general solution reads
$$\Phi(r)=\frac{C_1}{r} + C_2$$
with integration constants $C_1$ and $C_2$. Since there's no singularity at $r=0$, you must have the solution for $r<R$ (which I indicate with $\Phi_<$)
$$\Phi_<(r)=C_{2<}=\text{const}.$$
This implies that
$$\vec{E}_{<}=0.$$
For $r>R$ we can impose the condition that $\Phi_>(r) \rightarrow 0$ for $r \rightarrow 0$, which makes $C_{2>}=0$, and you get
$$\Phi_{>}(r)=\frac{C_{1>}}{r}.$$
To get $C_{1>}$ you have to use the boundary condition along the spherical shell, i.e.,
$$\vec{n} (\vec{E}_{>}(R)-\vec{E}_{<}(R)) =\vec{n} \cdot \vec{E}_{>}(R) = \sigma/\epsilon_0.$$
Here $\vec{n}=\vec{e}_r$ and thus
$$E_{>r}(R)=-\partial_r \Phi_{>}(R)=\frac{C_{1>}}{R^2}=\frac{\sigma}{\epsilon_0} \; \Rightarrow \; C_1=\frac{\sigma R^2}{\epsilon_0},$$
i.e., finally
$$\Phi_>(r)=\frac{\sigma R^2}{\epsilon_0 r}, \quad E_{r>}=\frac{\sigma R^2}{\epsilon_0 r^2}.$$
With $\sigma=q/(4 \pi R^2)$ you get the Coulomb field of a point charge $q$ in the origin (but of course only outside the spherical shell).

 

[warhammer]

The great thing of vector calculus is that it deals with invariant quantities. Indeed the physics must not depend on the coordinates you arbitrarily choose to describe a problem. It's clear that a good choice in the beginning can tremendously simplify the solution. Particularly you should use the coordinates that are adapted to possibly present symmetries. That's why one works out also the generally covariant formalism, which works for any choice of generalized coordinates. In introductory textbooks you usually only consider the special case of curvilinear orthogonal coordinates, where the tangent vectors along the coordinate lines are all mutually orthogonal to each other, and then you also choose the normalized tangent vectors as the local basis vectors.

Nevertheless in the cases discussed above, it's more convenient to use Cartesian coordinates and just use parametrizations of the geometry of the charge distributions in terms of generalized coordinates (parameters).

The reason for Prob. 2.6 is that the author has restricted himself to the simplest special symmetrical case, i.e., the field along the symmetry axis of the disc. The general solution is much more complicated and involves even some elliptic functions I guess. Then you should rather work in cylindrical coordinates only.

For this special case, it even makes sense to blindly use the standard integral solution with the Green's function as given in your solution.

The reason for Prob. 2.7 is that you can restrict yourself to calculate the field along the $z$-axis, because everything is spherically symmetric, i.e., you get the general solution by calculating this special case, and then you know the solution everywhere due to symmetry.

Here, I'd however say, it's not good advice to use the integral. It's much easier to use the differential form in spherical coordinates. It's clear that the potential must be a function of $r$ only, and then with the Laplacian in spherical coordinates you simply have
$$\frac{1}{r} [r \Phi(r)]''=\rho/\epsilon_0.$$
For the spherical shell of radius $R$ with a homogeneous surface charge density, $\sigma$ you have
$$[r \Phi(r)]''=0$$
except at $r=R$, where you have to adjust the singularities of your solution to the given surface charge distribution. So except at $r=R$ the general solution reads
$$\Phi(r)=\frac{C_1}{r} + C_2$$
with integration constants $C_1$ and $C_2$. Since there's no singularity at $r=0$, you must have the solution for $r<R$ (which I indicate with $\Phi_<$)
$$\Phi_<(r)=C_{2<}=\text{const}.$$
This implies that
$$\vec{E}_{<}=0.$$
For $r>R$ we can impose the condition that $\Phi_>(r) \rightarrow 0$ for $r \rightarrow 0$, which makes $C_{2>}=0$, and you get
$$\Phi_{>}(r)=\frac{C_{1>}}{r}.$$
To get $C_{1>}$ you have to use the boundary condition along the spherical shell, i.e.,
$$\vec{n} (\vec{E}_{>}(R)-\vec{E}_{<}(R)) =\vec{n} \cdot \vec{E}_{>}(R) = \sigma/\epsilon_0.$$
Here $\vec{n}=\vec{e}_r$ and thus
$$E_{>r}(R)=-\partial_r \Phi_{>}(R)=\frac{C_{1>}}{R^2}=\frac{\sigma}{\epsilon_0} \; \Rightarrow \; C_1=\frac{\sigma R^2}{\epsilon_0},$$
i.e., finally
$$\Phi_>(r)=\frac{\sigma R^2}{\epsilon_0 r}, \quad E_{r>}=\frac{\sigma R^2}{\epsilon_0 r^2}.$$
With $\sigma=q/(4 \pi R^2)$ you get the Coulomb field of a point charge $q$ in the origin (but of course only outside the spherical shell).

Thank you for such a detailed response sir. But if you do not mind, could you dumb it down a little for me and elaborate.. I think I absorbed the crux of what you conveyed but still would like to iron any deficiencies. Especially because I still feel I have been unable to intuitively gauge the distinctions between the two. A sincere request

 

[vanhees71]

What specifically is unclear in the above calculation? What do you mean by "distinctions between the two" (which "two")?

 

[warhammer]

What specifically is unclear in the above calculation?

My question was we formulate our relationships in spherical or cylindrical systems (depending upon which symmetry is convenient in the particular case), then have it multiplied with $cos \theta$ which rinses out the result as a vector in $\hat z$ direction (Cartesian system). How is this "shift" between systems occurring?

I well understand that due to symmetry operations field in both cases "must" be along $\hat z$ as x,y components cancel out but we still magically shift between 2 different coordinate systems. How does is this happen is what my question was since I see this happening in a lot of EM problems of such cohorts.

What do you mean by "distinctions between the two" (which "two")?

Distinctions between Problem 2.6 & 2.7 because I did not understand what you meant in your response...

 

[Orodruin]

There is no magic going on. Just coordinate transformations. You are aware that one set of coordinates can be expressed as functions of another, yes?

 

[warhammer]

There is no magic going on. Just coordinate transformations. You are aware that one set of coordinates can be expressed as functions of another, yes?

Yes. I am aware of those as mentioned in #1 below. But I will explain where I have a doubt. For transforming a vector along $\hat r$ along $\hat z$ one can multiply the same with $cos\theta$. But $\theta$ is the Polar Angle and that should be used to do the transformation. Instead in 2.7, $\cosα$ is used, and that stumps me.

EDIT 1: $\hat r = (...) \hat x + (...) \hat y + cos\theta \hat z$ and $\hat z = cos\theta \hat r - (..) \hat theta$
Is the interplay between 2 coordinate systems used in P2.7 explained by the above relationships (given that we take the field to be emanating radially outward from vantage point of spherical coordinates?)

 

[Orodruin]

Yes. I am aware of those as mentioned in #1 below. But I will explain where I have a doubt. For transforming a vector along $\hat r$ along $\hat z$ one can multiply the same with $cos\theta$. But $\theta$ is the Polar Angle and that should be used to do the transformation. Instead in 2.7, $\cosα$ is used, and that stumps me.

I think you are mixing up $\hat r$ and $\hat{\mathscr{r}}$.

 

[vanhees71]

My question was we formulate our relationships in spherical or cylindrical systems (depending upon which symmetry is convenient in the particular case), then have it multiplied with $cos \theta$ which rinses out the result as a vector in $\hat z$ direction (Cartesian system). How is this "shift" between systems occurring?

It's still not clear to me, what you mean. The point is that the physics is independent of the choice of the coordinate system. There are one-to-one mappings between the different coordinates (in the range, where they are well defined) and the physical quantities do not depend on which coordinates you use. That's how vector (or tensor) calculus is formulated. What do you mean by "rinses out the result as a vector"?

The definition of spherical coordinates is usually given in its relation to Cartesian coordinates. The spherical coordinates are defined by separating out a polar axis, which is usually chosen as the $z$-axis of the Cartesian coordinate system:
$$\vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} r \sin \vartheta \cos \varphi \\ r \sin \vartheta \sin \varphi \\ r \cos \vartheta \end{pmatrix}.$$
Vectors (and vector fields) are then written as components wrt. the orthonormalized tangent vectors of the coordinate lines, $\vec{e}_r$, $\vec{e}_{\vartheta}$, $\vec{e}_{\varphi}$. The vectors are always the same, no matter in which coordinates you express them. E.g., for the electric field you have
$$\vec{E}=E_x \vec{e}_x + E_y \vec{e}_y + E_z \vec{e}_z= E_r \vec{e}_r + E_{\vartheta} \vec{e}_{\vartheta} + E_{\varphi} \vec{e}_{\varphi}.$$
When calculating the usual differential operations grad, div, and curl, you have to take into consideration that the basis vectors of the spherical coordinates also depend on the position, and that's how you get the formulae for the corresponding components of vectors and tensors in the spherical coordinates which look more complicated than in Cartesian coordinates.

I well understand that due to symmetry operations field in both cases "must" be along $\hat z$ as x,y components cancel out but we still magically shift between 2 different coordinate systems. How does is this happen is what my question was since I see this happening in a lot of EM problems of such cohorts.

Distinctions between Problem 2.6 & 2.7 because I did not understand what you meant in your response...

In Problem 2.6 the symmetry used is specific only for the special case that the field argument $\vec{r}$ is on the $z$ axis. In Problem 2.7 you use the symmetry for any field argument.

Judging from #1 your problem seems to be that you don't clearly write out what you really calculate. It seems as if you want to calculate everything in Cartesian coordinates by using the integral for the electric field,
$$\vec{E}(\vec{r})=\int_{S_R} \mathrm{d}^2 f' \frac{\sigma(\vec{r}')(\vec{r}-\vec{r}')}{4 \pi \epsilon_0 |\vec{r}-\vec{r}'|^3}$$
with $\vec{r}=(0,0,z)$.

To calculate the integral along the spherical shell we introduce the usual spherical coordinates $(\vartheta,\varphi)$:
$$\vec{r}'=R \begin{pmatrix} \sin \vartheta \cos \varphi \\ \sin \vartheta \sin \varphi \\ \cos \vartheta \end{pmatrix}.$$
Then we need the surface element
$$\mathrm{d}^2 f = |\partial_{\vartheta} \vec{r}' \times \partial_{\varphi} \vec{r}'| \mathrm{d} \vartheta \mathrm{d} \varphi =R^2 \sin \vartheta \mathrm{d} \vartheta \mathrm{d} \varphi.$$
Then
$$\vec{r}-\vec{r}'=\begin{pmatrix} -R \sin \vartheta \cos \varphi \\ -R \sin \vartheta \cos \varphi \\ z-R \cos \vartheta \end{pmatrix}.$$
and
$$|\vec{r}-\vec{r}'|^2=\vec{r}^2 + \vec{r}^{\prime 2} - 2 \vec{r} \cdot \vec{r}' = z^2 + R^2 -2 z R \cos \vartheta.$$
Plugging all this in the integral and using $\sigma(\vec{r}')=\text{const}$ you get
$$\vec{E}(\vec{r}) = \frac{\sigma R^2}{4 \pi \epsilon_0} \int_0^{\pi} \mathrm{d} \vartheta \int_0^{2 \pi} \mathrm{d} \varphi \sin \vartheta \begin{pmatrix} -R \sin \vartheta \cos \varphi \\ -R \sin \vartheta \cos \varphi \\ z-R \cos \vartheta \end{pmatrix} \frac{1}{(z^2 + R^2 - 2 z R \cos \vartheta)^{3/2}}.$$
Now we do the integral over $\varphi$. This gives $E_x=E_y=0$, because integrating $\cos \varphi$ or $\sin \varphi$ over any interval of the length $2 \pi$ gives 0. For the $E_z$ component you get just a factor of $2 \pi$, because the integrand for this component doesn't depend on $\varphi$. Thus we have
$$\vec{E}(\vec{r}) = \frac{\sigma R^2}{2 \epsilon_0} \int_0^{\pi} \mathrm{d} \vartheta \sin \vartheta \begin{pmatrix} 0 \\ 0 \\ z-R \cos \vartheta \end{pmatrix} \frac{1}{(z^2 + R^2 - 2 z R \cos \vartheta)^{3/2}}.$$
Now we substitute $u=\cos \vartheta$:
$$\vec{E}(\vec{r}) = \frac{\sigma R^2}{2 \epsilon_0} \int_{-1}^1 \mathrm{d} u \begin{pmatrix} 0 \\ 0 \\ z-R u \end{pmatrix} \frac{1}{(z^2+R^2-2zR u)^{3/2}}.$$
This we can rewrite as
$$E_z(\vec{r})=-\frac{\sigma R^2}{2 \epsilon_0} \partial_z \int_{-1}^1 \mathrm{d} u \frac{1}{\sqrt{z^2+R^2-2z R u}}=\frac{\sigma R^2}{2 \epsilon_0} \partial_z \left [\sqrt{z^2+R^2-2zR u}{R z} \right]_{u=-1}^{u=1} = \frac{\sigma R}{2\epsilon_0} \partial_z \left (\sqrt{(z-R)^2}-\sqrt{(z+R)^2} \right )/z.$$
Now for $z>R$ you finally get
$$E_z(\vec{r}) = \frac{\sigma R^2}{\epsilon_0 z^2}$$
and for $0<z<R$
$$E_z(\vec{r})=0.$$