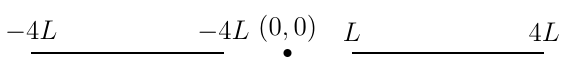Electric field of a finite linear distribution of charge

[darioslc]

Homework Statement

Get the electric field and the potential due to wire of length 3L in the point (0,0)

Relevant Equations

E definition and potencial:
$$\vec{E}(x,y)=\frac1{4\pi\varepsilon_0}\int\frac{dq}{(r-r')^{2}}\hat{r}$$
$$E=-\nabla V$$

Hello! I do it for definition because Gauss's law not possible.
I use cartesian coordinates:
$$dq=\lambda dx'\text{because is only in x direction}$$

$$\vec{r'}=(x',0)$$
$$\vec{r}-\vec{r'}=(x-x',y)$$
$$\hat{r}=\frac{(x-x',y)}{\sqrt{(x-x')^{2}+y^{2}}}$$

$$\vec{E}(x,y)=\frac1{4\pi\varepsilon_0}\int\frac{\lambda}{\sqrt{(x-x')^{2}+y^2}^2}\frac{(x-x',y)}{\sqrt{(x-x')^{2}+y^{2}}}dx'$$
like in $y=0$, only survive one integral, in (0,0):

$$\vec{E}(x,y)=\frac1{4\pi\varepsilon_0}\int\frac{\lambda}{\sqrt{(x')^{2}}^2}\frac{-x'}{\sqrt{x'^{2}}}dx'$$

$$\vec{E}(x,y)=-\frac1{4\pi\varepsilon_0}\lambda\int\frac{x'}{|x'|^3}dx'$$

now like x'>0 $\vec{E}(0,0)=-\frac{1}{4\pi\varepsilon_0}\lambda\int\frac{1}{x'^{2}}dx'\hat{x}$
then $\vec{E}(0,0)=\frac{1}{4\pi\varepsilon_0}\lambda\frac{3}{4L}$

Then is similar for the other wire, but I get with opposite sign, therefore E(0,0)=0

My doubt is the potencial, I need the general expression for E then integrate both components and evaluate in (0,0) or only will constant in (0,0)?

Thanks a lot

 

[haruspex]

Your working is confusing because

1. You omitted to mention where the wire is in relation to (0,0). (I gather from the diagram it is from (L,0) to (4L,0).)
2. The diagram shows a second wire.
3. You haven’t shown the integration boundaries.
4. The problem is in one dimension. Why refer to (x,y)?

 

[TSny]

$$\vec{E}(x,y)=\frac1{4\pi\varepsilon_0}\int\frac{\lambda}{\sqrt{(x-x')^{2}+y^2}^2}\frac{(x-x',y)}{\sqrt{(x-x')^{2}+y^{2}}}dx'$$

On the left side you have the vector $\vec{E}(x,y)$, but on the right side you have the x-component of $\vec{E}(x,y)$ [EDIT: Nevermind, I think this is OK]

now like x'>0 $\vec{E}(0,0)=-\frac{1}{4\pi\varepsilon_0}\lambda\int\frac{1}{x'^{2}}dx'\hat{x}$
then $\vec{E}(0,0)=\frac{1}{4\pi\varepsilon_0}\lambda\frac{3}{4L}$

Did you leave out the unit vector $\hat x$ on the right side in the second line above?
Does your answer correspond to the direction that you would expect for $\vec E(0,0)$?

Then is similar for the other wire, but I get with opposite sign, therefore E(0,0)=0

Ok. You could have used this symmetry argument at the beginning to conclude $E(0,0) = 0$ without doing any calculation.

My doubt is the potencial, I need the general expression for E then integrate both components and evaluate in (0,0) or only will constant in (0,0)?

You cannot get $V$ by integrating $\vec{\nabla} V= -\vec E$, since that would require knowing $E$ at points other than the origin.

Can you set up an expression for the potential $dV$ at the origin due to an infinitesimal element of charge $dq$ of the system? Then integrate to get the net $V$ due to all the elements of charge.

 

[TSny]

You cannot get $V$ by integrating $\vec{\nabla} V= -\vec E$, since that would require knowing $E$ at points other than the origin.

If you want to integrate $\vec{\nabla} V= -\vec E$ to get $V$ at the origin, then you could first find a general expression for $\vec E(0,y)$ at points on the y-axis. Then integrate $\vec E(0,y) \cdot \vec{dr} = E_y(0,y) dy$ along the y-axis.

It's a nice exercise, but not as easy as finding $V$ at the origin by directly integrating $dV$ for elements of charge $dq$.

 

[PhDeezNutz]

These are my cursory thoughts. I haven’t done the problem all the way out.

Instead of doing this by brute force integration as the configuration exists (some integration is eventually inevitable) I would come up with an ancillary configuration.

I would start by filling in the gap with a complete line charge of $\lambda$ and find the potential at said point of interest.

Then I would somehow correct for adding that line segment that wasn’t there to begin with……somehow…..can you think how?

 

[kuruman]

These are my cursory thoughts. I haven’t done the problem all the way out.

Instead of doing this by brute force integration as the configuration exists (some integration is eventually inevitable) I would come up with an ancillary configuration.

I would start by filling in the gap with a complete line charge of $\lambda$ and find the potential at said point of interest.

Then I would somehow correct for adding that line segment that wasn’t there to begin with……somehow…..can you think how?

If integration is inevitable, then, since the electric field is zero at the origin by symmetry, the integral to do is $$V(x,y)=k\lambda \int_L^{4L}\frac{dx'}{[(x-x')^2+y^2]^{1/2}}.$$ The integral simplifies tremendously at the origin and the force needed to do it is hardly brutish.

 

[PhDeezNutz]

If integration is inevitable, then, since the electric field is zero at the origin by symmetry, the integral to do is

V(x,y)=kλ∫4LLdx′[(x−x′)2+y2]1/2.V(x,y)=kλ∫L4Ldx′[(x−x′)2+y2]1/2.​

The integral simplifies tremendously at the origin and the force needed to do it is hardly brutish.

Alright that's fair. Should have said instead that if you can come up with an ancillary configuration then you can readily use well known expressions without having to integrate.

Edit: but i guess it's really not that hard to integrate from the get go.

 

[darioslc]

Thanks! finally I do using definition of potential:
$$V(x,y)=\frac1{4\pi\varepsilon_0}\int\frac{dq}{|\vec{r}-\vec{r'}|}$$
in $(0,y)$
$$V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\int\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'$$
adding two potential due to wires:
$$V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+y^{2}})(5R+\sqrt{25R^{2}+y^{2}})}{(-5R+\sqrt{25R^{2}+y^{2}})(R+\sqrt{R^{2}+y^{2}})}\right)$$

more than easy that using of gradient.

 

[TSny]

$$V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\int\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'$$

What are the lower and upper limits of the integral?

adding two potential due to wires:
$$V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+y^{2}})(5R+\sqrt{25R^{2}+y^{2}})}{(-5R+\sqrt{25R^{2}+y^{2}})(R+\sqrt{R^{2}+y^{2}})}\right)$$

This is not correct. I think you must have used incorrect limits for the integration.

You are only asked to find $V$ at the origin. So, you only need $V(0,0)$.

 

[kuruman]

You are only asked to find $V$ at the origin. So, you only need $V(0,0)$.

And if you set $y=0$ in your expression in post #8, you get
$$V(0,0)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+0})(5R+\sqrt{25R^{2}+0})}{(-5R+\sqrt{25R^{2}+0})(R+\sqrt{R^{2}+0})}\right).$$Look at the numerator and denominator. What happens to them when you simplify further?

 

[darioslc]

And if you set $y=0$ in your expression in post #8, you get
$$V(0,0)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+0})(5R+\sqrt{25R^{2}+0})}{(-5R+\sqrt{25R^{2}+0})(R+\sqrt{R^{2}+0})}\right).$$Look at the numerator and denominator. What happens to them when you simplify further?

Yes diverge but, is it because the point y=0 is in the same line that wires? ie, the electric field close to (0,0) is very extreme (ideally), I add the graph that illustrate both

 

[PhDeezNutz]

Let's take a moment to acknowledge the effort that @darioslc has put in. Not only showing his analytical calculations but numerical/computational results. This example should be followed by every first time poster.

Edit: please ignore my previous posts. I had originally thought that the problem was to find the potential on the y-axis for general y. I now see that it is not. Direct integration is absolutely the best way to go as @kuruman and @TSny have stated.

 

[kuruman]

Yes diverge but, is it because the point y=0 is in the same line that wires?

I think it's because you made a mistake in deriving the equation for $V(x,y).$ The total charge on each wire segment is $Q=3\lambda L$. If you place two point charges $Q$ at $x = \pm L$, the potential at the origin will be finite and equal to $V_0=2\times\dfrac{k(3\lambda L)}{L}=6k\lambda$. Stretching the point charges back into linear charge distributions will result in a potential that is less than this value because there will be more charge farther out from the origin. Thus, $V_0=6k\lambda L$ is an upper limit and there is no divergence.

 

[TSny]

darioslc wrote $$V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+y^{2}})(5R+\sqrt{25R^{2}+y^{2}})}{(-5R+\sqrt{25R^{2}+y^{2}})(R+\sqrt{R^{2}+y^{2}})}\right)$$

Note that this expression does not diverge as $y \rightarrow 0$ as you can show by taking the limit.

Nevertheless, the above expression for $V(0, y)$ is not correct.

@darioslc: can you show more steps in getting this result? In particular, what did you use for the limits of integration? Also, what does the symbol $R$ represent?

To get $V(0,0)$, you can let $y = 0$ before integrating.

 

[darioslc]

darioslc wrote $$V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+y^{2}})(5R+\sqrt{25R^{2}+y^{2}})}{(-5R+\sqrt{25R^{2}+y^{2}})(R+\sqrt{R^{2}+y^{2}})}\right)$$

Note that this expression does not diverge as $y \rightarrow 0$ as you can show by taking the limit.

Nevertheless, the above expression for $V(0, y)$ is not correct.

@darioslc: can you show more steps in getting this result? In particular, what did you use for the limits of integration? Also, what does the symbol $R$ represent?

To get $V(0,0)$, you can let $y = 0$ before integrating.

Hello, may be there are mistakes I will check the calculus (but I do not find errors).

Sorry by confusion and delay in response, $R$ is the $L$ that I had put in the first drawing.

The limits of integration was:
$$\begin{align*}
V(0,y)=&\frac1{4\pi\varepsilon_0}\lambda\int\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'\,\text{ for each wires:}\\
V(0,y)_{-}=&\frac1{4\pi\varepsilon_0}\lambda\int_{-5R}^{-R}\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'=\frac1{4\pi\varepsilon_0}\lambda\left(\ln(x'+\sqrt{x'^2+y^2}\right)_{-5R}^{-R}\\
V(0,y)_{+}=&\frac1{4\pi\varepsilon_0}\lambda\int_{R}^{5R}\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'=\frac1{4\pi\varepsilon_0}\lambda\left(\ln(x'+\sqrt{x'^2+y^2}\right)_{R}^{5R}\\
V(0,y)_{-}=&\frac1{4\pi\varepsilon_0}\lambda(\ln(-R+\sqrt{R^{2}+y^{2}})-\ln(-5R+\sqrt{25R^{2}+y^{2}}))\\
V(0,y)_{+}=&\frac1{4\pi\varepsilon_0}\lambda(\ln(5R+\sqrt{25R^{2}+y^{2}})-\ln(R+\sqrt{R^{2}+y^{2}}))
\end{align*}
$$
yes it's true not diverge, I think that because quickly saw the 0/0 but not calculated (great self mistake), the limit when $y->0$ is 25.

Now when add the two potential:
$$
V(0,y)=\frac1{4\pi\varepsilon_0}\lambda\ln\left(\frac{(-R+\sqrt{R^{2}+y^{2}})(5R+\sqrt{25R^{2}+y^{2}})}{(-5R+\sqrt{25R^{2}+y^{2}})(R+\sqrt{R^{2}+y^{2}})}\right)
$$

 

[PhDeezNutz]

I think you're trying to be too general which is admirable but overkill for this problem. Instead of finding the potential for a general point on the y-axis why not just plug in the values you need from the get go as suggested in posts #6 and #9?

For general $\left(x,y \right)$ you have
$V \left(x ,y \right) = 2 \frac{ \lambda}{4 \pi \epsilon_0} \int_{L}^{4L} \frac{1}{\sqrt{\left(x - x'\right)^2 + \left(y - y' \right)^2}} \, dx'$

What values should you plug in for $x,y,$ and $y'$?

Once you do that how much simpler does your work become?

 

[TSny]

The limits of integration was:
$$V(0,y)_{+}=\frac1{4\pi\varepsilon_0}\lambda\int_{R}^{5R}\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'$$

Shouldn’t the upper limit be $4R$?

 

[darioslc]

Shouldn’t the upper limit be ?

Yes, I'm sorry is early morning here and a bit tired.

Finally I think I already understood. Thanks a lot

 

[kuruman]

$$
\frac1{4\pi\varepsilon_0}\lambda\int_{-5R}^{-R}\frac{1}{\sqrt{x'^{2}+y^{2}}}dx'=\frac1{4\pi\varepsilon_0}\lambda\left(\ln(x'+\sqrt{x'^2+y^2}\right)_{-5R}^{-R}
$$

Please show how you got the right side to be equal to the left hand side. This is where your mistake is. The potentials that you have called $V(0,y)_{+}$ and $V(0,y)_{-}$ must be equal by symmetry.

If you have a single line of charge the potential at distance $L$ from its right end is the same as the potential at distance $L$ from the left end. Call that potential $V_0$. If you put two lines of charge arranged as in this problem, at the point in the middle (the origin) the potential will be $V(0,0)=2V_0$.