arestes
- 84
- 4
Hi.
I was reading about conductors in electrostatic equilibrium and how it makes sense that they have zero electric field inside the material even when an external charge is brought near. The charge density of the material just rearranges itself to cancel. Then I searched for hollow conductors since they behave differently.
However, the derivations of the fact that there is zero field inside a conductor (both hollow and solid) uses symmetry.
Using Gauss' law and this symmetry, when there's no charge outside, it can easily be seen that the magnitude of the field is the same at a specified distance of the center and it clearly means that a gaussian surface enclosing no charge implies a zero field.
I am worried of this last step because when an external charge is brought near, there is no spherical symmetry anymore. ¿Is the field inside shielded completely? Or, ¿is this just an approximation of a "Faraday Cage"? (does it work the same when the sphere is hollow and when it's solid?).
I found a Wiley resource that says it's not zero:

But I also found another resource (both on google) that asks the same but, the answer it gives is zero:
https://www.liveworksheets.com/oi1233136al
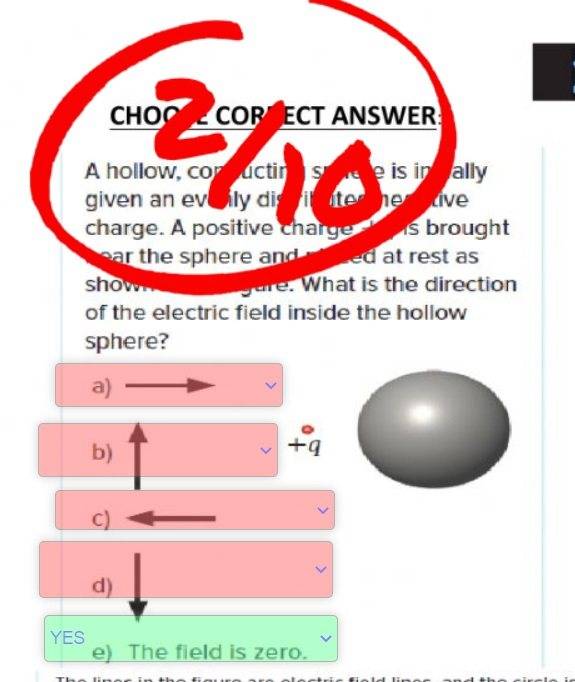
(By the way, this other question is in many websites but I'm not sure what book this has been taken from, does anyone know?).
So... does a (hollow or solid) spherical conductor with an external point charge completely shield off electric fields inside it?
Also, I have a feeling it doesn't. I read wikipedia's article about image charges with this method of "mirror images" and it's supposed to act as if there was another charge inside of opposite sign. Does this work with solid or hollow. I couldn't find.
ThanksI
I was reading about conductors in electrostatic equilibrium and how it makes sense that they have zero electric field inside the material even when an external charge is brought near. The charge density of the material just rearranges itself to cancel. Then I searched for hollow conductors since they behave differently.
However, the derivations of the fact that there is zero field inside a conductor (both hollow and solid) uses symmetry.
Using Gauss' law and this symmetry, when there's no charge outside, it can easily be seen that the magnitude of the field is the same at a specified distance of the center and it clearly means that a gaussian surface enclosing no charge implies a zero field.
I am worried of this last step because when an external charge is brought near, there is no spherical symmetry anymore. ¿Is the field inside shielded completely? Or, ¿is this just an approximation of a "Faraday Cage"? (does it work the same when the sphere is hollow and when it's solid?).
I found a Wiley resource that says it's not zero:
But I also found another resource (both on google) that asks the same but, the answer it gives is zero:
https://www.liveworksheets.com/oi1233136al
(By the way, this other question is in many websites but I'm not sure what book this has been taken from, does anyone know?).
So... does a (hollow or solid) spherical conductor with an external point charge completely shield off electric fields inside it?
Also, I have a feeling it doesn't. I read wikipedia's article about image charges with this method of "mirror images" and it's supposed to act as if there was another charge inside of opposite sign. Does this work with solid or hollow. I couldn't find.
ThanksI
Attachments
Last edited by a moderator: