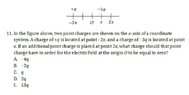Tesla In Person
- 34
- 13
- Homework Statement
- Find the value of the charge placed at the point that makes the electric field 0.
- Relevant Equations
- Electric field: Kq /r^2
I got E. 13q as the answer. That is what i did: The electric field due to +q at origin 0 should equal the electric fields of charges -3q and the new charge placed at 2x. So applying the equation above like this; k*(q) / (2^2) = -3q*k + (k*C)/ 4 solving for C the new charge added, gives 13q. I don't know if it's correct because i don't have the answer to this question . Can you please check my working thanks.