Electric field vector equation: Finding the neutral point for two charges

[tellmesomething]

Homework Statement

Position vector of q is î+j(hat)+2k(hat) and position vector of 4q is 2î+j(hat) +3k(hat). Find the position vector of neutral point.

Relevant Equations

Electric field vector due to q+Electric field vector due to 4q=0

This is the general suggested approach given in a textbook.

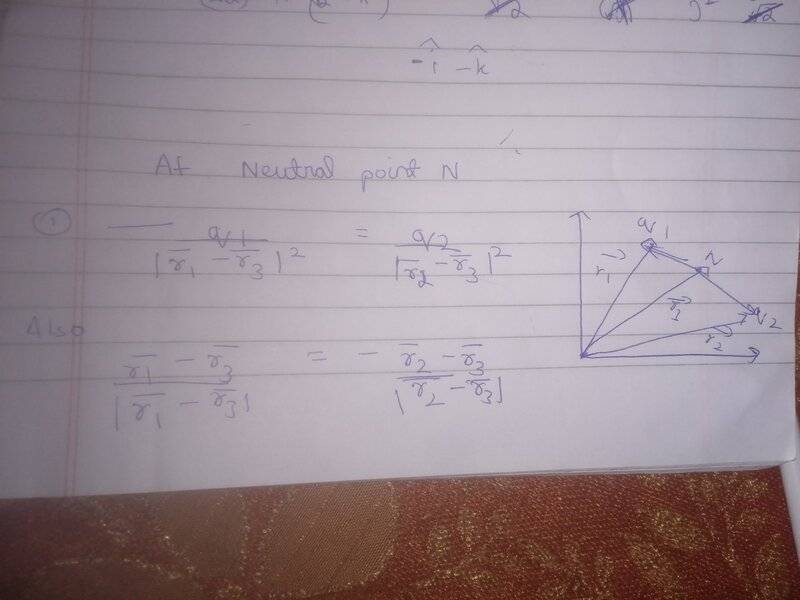
My question is why can I not directly write it in vector form?
E1 vector + E2 vector =0 should be valid no?
Why are they choosing to write E1 mag + E2 mag=0
Then find a vector form
Then convert the magnitude equation into a vector one?

What I did is:

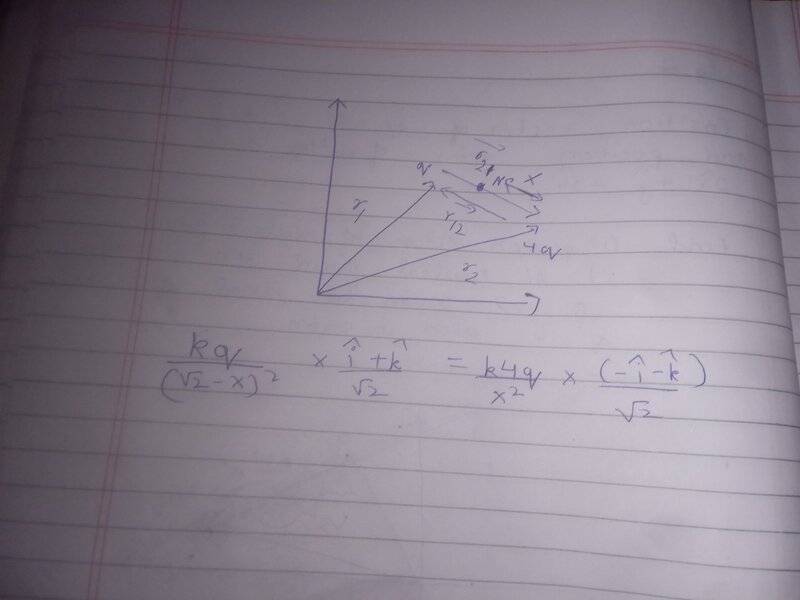
I know we cannot cancel vectors so this just might be the worst approach but I dont get how we used the first approach just like that....

 

[kuruman]

E1 vector + E2 vector =0 should be valid no?

It should be valid if you know how to write the electric field at an arbitrary point P using unit vector notation. You start by writing the position vector that you are looking for
$\mathbf r=x~\mathbf{\hat i}+y~\mathbf{\hat j}+z~\mathbf{\hat k}$. The expression for the electric field at P is $$\mathbf E(\mathbf r)=\frac{1}{4\pi\epsilon_0}\sum_{i=1}^2\frac{q_i(\mathbf r-\mathbf r'_i)}{|\mathbf r-\mathbf r'_i|^3}.$$The primed coordinates are those of the given charges.

The textbook's solution is much easier to implement because you have only two charges which means that the neutral point must be on the line joining them. Do you see why?

 

[tellmesomething]

It should be valid if you know how to write the electric field at an arbitrary point P using unit vector notation. You start by writing the position vector that you are looking for
$\mathbf r=x~\mathbf{\hat i}+y~\mathbf{\hat j}+z~\mathbf{\hat k}$. The expression for the electric field at P is $$\mathbf E(\mathbf r)=\frac{1}{4\pi\epsilon_0}\sum_{i=1}^2\frac{q_i(\mathbf r-\mathbf r'_i)}{|\mathbf r-\mathbf r'_i|^3}.$$The primed coordinates are those of the given charges.

The textbook's solution is much easier to implement because you have only two charges which means that the neutral point must be on the line joining them. Do you see why?

You say that the primed coordinates are of the given charge....
What do you mean by that? I should have to put r' as the position vector of the neutral point...
Also I would like to go through this solution if possible I understand the textbook might be easier but never two many...

 

[kuruman]

You say that the primed coordinates are of the given charge....
What do you mean by that? I should have to put r' as the position vector of the neutral point...
Also I would like to go through this solution if possible I understand the textbook might be easier but never two many...

I mean
$q_1=q~$ at position $~\mathbf r'_1=\mathbf{\hat i}+\mathbf{\hat j}+2~\mathbf{\hat k}$
$q_2=4q~$ at position $~\mathbf r'_2=2~\mathbf{\hat i}+\mathbf{\hat j}+3~\mathbf{\hat k}$
Then just substitute. For example for $q_1$
$(\mathbf r-\mathbf r'_1)=(x-1)~\mathbf{\hat i}+(y-1)~\mathbf{\hat j}+(z-2)~\mathbf{\hat k}$
$|\mathbf r-\mathbf r'_1|^3=\left[(x-1)^2+(y-1)^2+(z-2)^2 \right]^{3/2}$
and similarly for $q_2$. Add the two terms in the summation, set the sum equal to zero and solve for the coordinates $(x,y,z).$

 

[tellmesomething]

I mean
$q_1=q~$ at position $~\mathbf r'_1=\mathbf{\hat i}+\mathbf{\hat j}+2~\mathbf{\hat k}$
$q_2=4q~$ at position $~\mathbf r'_2=2~\mathbf{\hat i}+\mathbf{\hat j}+3~\mathbf{\hat k}$
Then just substitute. For example for $q_1$
$(\mathbf r-\mathbf r'_1)=(x-1)~\mathbf{\hat i}+(y-1)~\mathbf{\hat j}+(z-2)~\mathbf{\hat k}$
$|\mathbf r-\mathbf r'_1|^3=\left[(x-1)^2+(y-1)^2+(z-2)^2 \right]^{3/2}$
and similarly for $q_2$. Add the two terms in the summation, set the sum equal to zero and solve for the coordinates $(x,y,z).$

Oops okay. I did not read your initial post though you did mention that the vector at point p is r. My bad. Anyways I did something similar to this in my approach I just took an x length to subtract. Anyways i ll see whats wrong with that...thankyou

 

[tellmesomething]

I mean
$q_1=q~$ at position $~\mathbf r'_1=\mathbf{\hat i}+\mathbf{\hat j}+2~\mathbf{\hat k}$
$q_2=4q~$ at position $~\mathbf r'_2=2~\mathbf{\hat i}+\mathbf{\hat j}+3~\mathbf{\hat k}$
Then just substitute. For example for $q_1$
$(\mathbf r-\mathbf r'_1)=(x-1)~\mathbf{\hat i}+(y-1)~\mathbf{\hat j}+(z-2)~\mathbf{\hat k}$
$|\mathbf r-\mathbf r'_1|^3=\left[(x-1)^2+(y-1)^2+(z-2)^2 \right]^{3/2}$
and similarly for $q_2$. Add the two terms in the summation, set the sum equal to zero and solve for the coordinates $(x,y,z).$

Another question in the book solution why is the $\vec r_{13}$ taken instead of $\vec r_{31}$. Shouldn't the position vector to the neutral point be taken from the charge instead of the other way around in the electric field equation?

 

[kuruman]

Another question in the book solution why is the $\vec r_{13}$ taken instead of $\vec r_{31}$. Shouldn't the position vector to the neutral point be taken from the charge instead of the other way around in the electric field equation?

I need to see the book solution and how $\vec r_{13}$ is defined and used. Please post a photo of the relevant section(s).

 

[tellmesomething]

I need to see the book solution and how $\vec r_{13}$ is defined and used. Please post a photo of the relevant section(s).

Sorry its the first photo in post #1 Thats the book solution im talking about. And $\vec r_{13}$ is nothing but $\vec r_1$ - $\vec r_3$

 

[kuruman]

Sorry its the first photo in post #1 Thats the book solution im talking about. And $\vec r_{13}$ is nothing but $\vec r_1$ - $\vec r_3$

First, that does not look like a book to me but handwritten notes.
Second, I don't see $\vec r_{13}$ or $\vec r_{13}$ anywhere. What is it that you wish to know when you ask

Another question in the book solution why is the $\vec r_{13}$ taken instead of $\vec r_{31}$. Shouldn't the position vector to the neutral point be taken from the charge instead of the other way around in the electric field equation?

Note that $|\vec r_{13}|=|\vec r_{31}|.$

 

[tellmesomething]

First, that does not look like a book to me but handwritten notes.
Second, I don't see $\vec r_{13}$ or $\vec r_{13}$ anywhere. What is it that you wish to know when you ask

Note that $|\vec r_{13}|=|\vec r_{31}|.$

Yes I cannot directly post the section from the book because its affiliated to a school who have sued others for pirating their books. I pirated it too so im trying to be safe:(

I understand that but in the immediate next line when they have equated the unit vectors they have used in the LHS :
$$ \frac { \vec r_1- \vec r_3} {|\vec r_1 - \vec r_3|} $$

And just beforce that in the LHS they are dealing with q1....so the unit vector of the position vector should be in the other direction I.e in the direction of the electric field lines from q1 to neutral point instead of neutral point to q1

 

[kuruman]

Yes I cannot directly post the section from the book because its affiliated to a school who have sued others for pirating their books. I pirated it too so im trying to be safe:(

I understand that but in the immediate next line when they have equated the unit vectors they have used in the LHS :
$$ \frac { \vec r_1- \vec r_3} {|\vec r_1 - \vec r_3|} $$

And just beforce that in the LHS they are dealing with q1....so the unit vector of the position vector should be in the other direction I.e in the direction of the electric field lines from q1 to neutral point instead of neutral point to q1

Yes, that should be the unit vector from $q_1$ to the point of interest. It is the direction of the electric field from 1 to 3 if $q_1$ is positive and from 3 to 1 if $q_1$ is negative.

 

[tellmesomething]

Yes, that should be the unit vector from $q_1$ to the point of interest. It is the direction of the electric field from 1 to 3 if $q_1$ is positive and from 3 to 1 if $q_1$ is negative.

Exactly but the book does the opposite so its wrong?

 

[kuruman]

Exactly but the book does the opposite so its wrong?

Yup, and not worth pirating.

 

[tellmesomething]

Yup, and not worth pirating.

LOL. Anyways thankyou very much :)

 

[tellmesomething]

Yup, and not worth pirating.

Sorry for disturbing but, on second thought im expected to convert the magnitude E equation of Electric field to a vector equation so if I write the position vector from the neutral point to the charges then only I can relate both the unit vectors as they would be equal and opposite ...on the other hand if I take the unit vectors from the charge to the neutral point (which is the direction of electric field) how will I relate it with the unit vector from charge q2 to the neutral point??

 

[kuruman]

In post #2 I show you the expression for the electric field at the neutral point $\mathbf r$.
In post #4 I showed you how to write the terms of the summation. The unit vectors are in the summation already (term in large parentheses below.) $$\frac{q_i(\mathbf r-\mathbf r'_i)}{|\mathbf r-\mathbf r'_i|^3}=\frac{q_i}{|\mathbf r-\mathbf r'_i|^2}\left(\frac{\mathbf r-\mathbf r'_i}{|\mathbf r-\mathbf r'_i|}\right).$$ Just set the summation equal to zero and solve for $(x,y,z).$

 

[tellmesomething]

In post #2 I show you the expression for the electric field at the neutral point $\mathbf r$.
In post #4 I showed you how to write the terms of the summation. The unit vectors are in the summation already (term in large parentheses below.) $$\frac{q_i(\mathbf r-\mathbf r'_i)}{|\mathbf r-\mathbf r'_i|^3}=\frac{q_i}{|\mathbf r-\mathbf r'_i|^2}\left(\frac{\mathbf r-\mathbf r'_i}{|\mathbf r-\mathbf r'_i|}\right).$$ Just set the summation equal to zero and solve for $(x,y,z).$

I was talking about the other approach I.e the book approach we were discussing and which you said is easier. There they equate the unit vectors in the second equation..

 

[kuruman]

I was talking about the other approach I.e the book approach we were discussing and which you said is easier. There they equate the unit vectors in the second equation..

Never mind the book's approach which may or may not be correct. You are asked to find the coordinates of the neutral point. How would you go about it? What is your strategy?

 

[tellmesomething]

Never mind the book's approach which may or may not be correct. You are asked to find the coordinates of the neutral point. How would you go about it? What is your strategy?

I went about it as I showed it in the second picture uploaded in post#1. I was a bit off maybe because I took the unit vector of the vector joining the two charges since I thought the vector joining the neutral point and the charge lies on the same line so the unit vector must be the same.....I understand this might be wrong but dont know why. I wrote the normal field equation and took x distance from the charge 4q to be the point where the neutral point lies, and then I multiplied it with their unit vectors and equated it. Mathematically I hit a wall since I would have to divide two vectors which is apparently not possible

 

[kuruman]

You are losing sight of your goal. You want two electric fields to get the zero vector $$\mathbf E_1+\mathbf E_2=0.$$ This means that one is the negative of the other,$$\mathbf E_1=-\mathbf E_2.$$ What is the angle between the two vectors when that is the case?

 

[tellmesomething]

You are losing sight of your goal. You want two electric fields to get the zero vector $$\mathbf E_1+\mathbf E_2=0.$$ This means that one is the negative of the other,$$\mathbf E_1=-\mathbf E_2.$$ What is the angle between the two vectors when that is the case?

180

 

[kuruman]

So at the neutral point, the two electric fields have an angle of 180° between them. Now look at the drawing below. It shows three regions in space, to the left of the charges (region I), between the charges (region II) and to the right of the charges (region III). Where do ou think the neutral point is and why? Add the neutral point and the two vectors at 180° to this drawing. I made it for this purpose and I don't mind if you pirate it. Then post your work.

 

[tellmesomething]

So at the neutral point, the two electric fields have an angle of 180° between them. Now look at the drawing below. It shows three regions in space, to the left of the charges (region I), between the charges (region II) and to the right of the charges (region III). Where do ou think the neutral point is and why? Add the neutral point and the two vectors at 180° to this drawing. I made it for this purpose and I don't mind if you pirate it. Then post your work.

View attachment 344397

I believe it would be on the line joining the two charges because this is where the field lines are anti parallel. It is most likely closer to the smaller charge because of the inverse square law

 

[kuruman]

I don't see any electric field lines at point N adding to give zero. Do you?

 

[tellmesomething]

I don't see any electric field lines at point N adding to give zero. Do you?

Pardon my drawing skills. In lower classes when we did neutral points it was a place with no field lines. Here its a bit different so I wasn't sure

 

[tellmesomething]

I don't see any electric field lines at point N adding to give zero. Do you?

From a quick google search though the first one is what it should look like https://images.app.goo.gl/M5LdU7dGmj2NTxtS9. Indeed no field lines

 

[kuruman]

From a quick google search though the first one is what it should look like https://images.app.goo.gl/M5LdU7dGmj2NTxtS9. Indeed no field lines

Not what I asked you to do. I asked to draw at point N the contributions to the electric field from each charge. In other words, at point N draw a field line representing the field from charge $q$ as if $4q$ were not there and then draw a second line at N representing the field from charge $4q$ as if $q$ were not there. Can you do that?

 

[tellmesomething]

Not what I asked you to do. I asked to draw at point N the contributions to the electric field from each charge. In other words, at point N draw a field line representing the field from charge $q$ as if $4q$ were not there and then draw a second line at N representing the field from charge $4q$ as if $q$ were not there. Can you do that?

 

[kuruman]

Very good. Note that this is another way of expressing zero at point N with vectors just like 3 + (-3) is another way of expressing zero with numbers. So when two vectors add to give zero, their magnitudes are the same and their directions are opposite. You put point N at some distance $x$ from charge $q$. Can you find the value of $x$ if you know that the separation between charges is $\sqrt{2}$?

 

[tellmesomething]

Very good. Note that this is another way of expressing zero at point N with vectors just like 3 + (-3) is another way of expressing zero with numbers. So when two vectors add to give zero, their magnitudes are the same and their directions are opposite. You put point N at some distance $x$ from charge $q$. Can you find the value of $x$ if you know that the separation between charges is $\sqrt{2}$?

Yes $$ \frac {kq} {x²}= \frac {k4q} {(√2-x)²} $$

 

[kuruman]

And what is the value of $x$ from that equation?

 

[tellmesomething]

Yes $$ \frac {kq} {x²}= \frac {k4q} {(√2-x)²} $$

I get x as $\frac {√2} {3}$ @kuruman

 

[tellmesomething]

And what is the value of $x$ from that equation?

Further I can multiply this with the unit vector and find the vevtor joining r2 and r3 as well as r3 and r1

 

[tellmesomething]

Further I can multiply this with the unit vector and find the vevtor joining r2 and r3 as well as r3 and r1

And from there its easy to find out the position vector r3

 

[kuruman]

And from there its easy to find out the position vector r3

Go ahead and do it.