Electric Fields with Motional EMF

[Rolls With Slipping]

Suppose I have a wire loop that I am moving away from a very long wire which carries a current upward and I want to find the induced current in the loop.

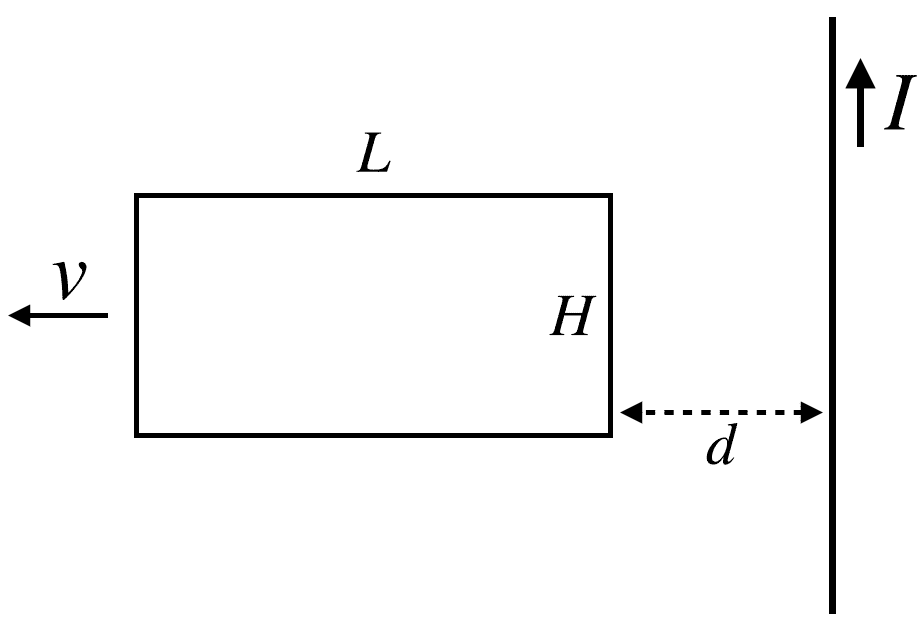The way I know how to approach this is with either Faraday's Law or motional EMF. My question concerns the motional EMF approach.

My understanding is to think of the magnetic force generating a separation of charges in the left and right wire segments. There will be a build up of positive charges on the top of the left and right segments and then a deficit of charge at the bottom of each.

This charge separation in turn produces an electric field and an associated electric potential difference is created for both the left and right wire segments. Since these potentials aren't the same there will be an induced counterclockwise current in the loop.

What I don't understand is why isn't the electric field produced in the top and bottom wires taken into account? The electric field for each wire segment should look this:

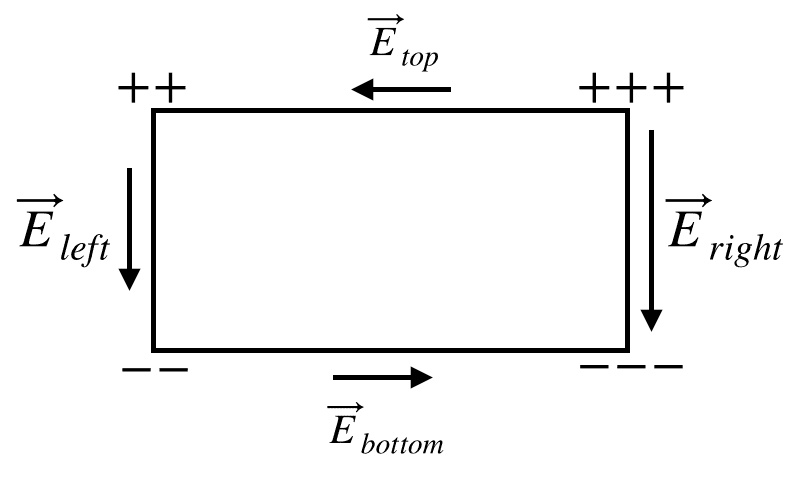The electric fields in the top and bottom segments will have an associated electric potential difference which would affect the current in the loop. Is it just that the assumption is the electric fields in the top and bottom segments are small compared to those in the left and right segments? Or maybe I'm missing something else?

 

[mfb]

The electric field in the horizontal wires is purely coming from the charge separation that happens in the vertical wires. If you give your wires a small resistance then you can calculate the potentials everywhere.

 

[nasu]

How do you calculate the current if you take it into account? And how if you don't? Who is not taking it into account?

 

[Delta2]

The top and bottom wires are special: They have two components of E-field that are perpendicular to each other.

One component is as you show it in your third picture but it is due to the charge separation on the vertical wires
The other component is perpendicular to the above and it is due to the charge separation that is happening inside these wires but this charge separation is also up to down (through the diameter of the top or bottom wire) and not left to right.

Remember the charge separation is happening according to the direction of $\vec{v}\times\vec{B}$.

 

[alan123hk]

According to the Lorentz force, when the entire rectangle moves to the left, the free charges inside the entire rectangular conductor will receive an upward force. Of course, the vertical conductor on the right is closer to the current source, so the force will be greater than the force on the left, so the final current direction will be counterclockwise. Please note that the charges inside the upper and lower horizontal conductors are subject to vertical forces.

In this case, applying Lorentz force will make calculating EMF relatively easy. Once the EMF is obtained, the current can be calculated according to Ohm's law.

 

[nasu]

@Delta2 My question was for the OP. I am not sure that he has a clear understanding of the question he asked. Sorry for not mentioning in the beginning.

 

[Rolls With Slipping]

Thanks everyone for your responds. Just to be clear, I understand (at least I think so) how to solve for the current. Here is how I would calculate the current using motional EMF and Faraday's Law.

There is charge separation in the left and right wire segments due to the Lorenz force. This charge separation continues until the magnetic and electric forces are balanced: $qvB = qE$. The potential difference across the wire segments can be calculated using the electric field, $\mathscr{E} = El = vlB$.

Assuming the loop has a resistance of R, the current induced would be:

$$ I = \frac{\mathscr{E}_{right}-\mathscr{E}_{left}}{R} = \frac{vH}{R}\left(\frac{\mu_o I}{2\pi d}-\frac{\mu_o I}{2\pi (d+L)}\right). $$

Performing the same analysis with Faraday's Law, leads to the same conclusion:

$$\Phi_m = \int \vec B \cdot d\vec a = \int\limits_{x_{left}}^{x_{right}} \frac{\mu_o I}{2 \pi x}(Hdx) = \frac{\mu_o I H}{2 \pi} \left( \ln(x_{right}) -\ln(x_{left}) \right), $$

$$I = \frac{\mathscr{E}}{R} = \frac{1}{R}\frac{d \Phi_m}{dt} = \frac{\mu_o I H}{2 \pi R} \left( \left. \frac{d}{dt} \left( \ln(x_{right}) \right) \right|_{x_{right} = d} - \left. \frac{d}{dt} \left( \ln(x_{left}) \right) \right|_{x_{left} = d + L} \right) = \frac{\mu_o I Hv}{2 \pi R}\left( \frac{1}{d} - \frac{1}{d + L} \right). $$

Both analyses yield the same result.

My main confusion has to do with the charge separation in the motional EMF analysis. The EMFs are calculated using the assumption that the magnetic and electric forces eventually balance each other, and then assume that the electric field has this constant value in the left and right segments. However the electric fields themselves don't have the same value which leads to different values for the EMFs. But if the electric fields don't have the same value then the amount of charge that is separated must be different too (which is what I was trying to show with my charge separation diagram in my original post). If the amount of charge is different then there will necessarily be some electric field in the top and bottom wires too, but then this would change the overall EMF in the loop.

I must not be thinking about the charge separation correctly. How exactly are the charges separated to achieve constant electric fields in the left and right wire segments, but no electric field in the top and bottom segments?

 

[Rolls With Slipping]

The top and bottom wires are special: They have two components of E-field that are perpendicular to each other.

One component is as you show it in your third picture but it is due to the charge separation on the vertical wires
The other component is perpendicular to the above and it is due to the charge separation that is happening inside these wires but this charge separation is also up to down (through the diameter of the top or bottom wire) and not left to right.

Remember the charge separation is happening according to the direction of $\vec{v}\times\vec{B}$.

Yes, that is right. If the wire has a finite thickness then there would be charge separation in the top and bottom wires which would generate a vertical electric field. However, this vertical electric field wouldn't contribute to the overall electric potential difference around the loop since the path of integration for $\int \vec E \cdot d \vec l$ would be perpendicular to the electric field. This is why you only need to consider the left and right segments.

 

[nasu]

There is an electric field in the horizontal wires. But this is not due to emfs in these wires. You can imagine the circuit as two batteries (vertical wires) connected by two resistors (horizontal wires). The batteries create potential differences across the resistors and electric fields in the resistors. These drive the current in the resistors. The batteries will have different emfs and they are connected in opposition. So the current in the horizontal wires is due to the fact that the two emfs are not equal. This corresponds to your different "charge separations" at the two ends. If the two emfs were equal there would be no current.

 

[Delta2]

My main confusion has to do with the charge separation in the motional EMF analysis. The EMFs are calculated using the assumption that the magnetic and electric forces eventually balance each other, and then assume that the electric field has this constant value in the left and right segments. However the electric fields themselves don't have the same value which leads to different values for the EMFs. But if the electric fields don't have the same value then the amount of charge that is separated must be different too (which is what I was trying to show with my charge separation diagram in my original post). If the amount of charge is different then there will necessarily be some electric field in the top and bottom wires too, but then this would change the overall EMF in the loop.

I must not be thinking about the charge separation correctly. How exactly are the charges separated to achieve constant electric fields in the left and right wire segments, but no electric field in the top and bottom segments?

The electric field from charge separation is conservative so its integral around a closed loop is always zero. The motional EMF in your example is not the integral $\oint \vec{E}\cdot d\vec{l}$ which is zero, it is rather the integral $\oint (\vec{v}\times\vec{B})\cdot d\vec{l}$ around the same loop which is not zero. The difference between those two comes from the top and bottom segments where the $\int_{top} \vec{E}\cdot d\vec{l}\neq 0$ but $\int_{top}(\vec{v}\times\vec{B})\cdot d\vec{l}=0$ (and similar for the bottom wire).

 

[alan123hk]

The EMFs are calculated using the assumption that the magnetic and electric forces eventually balance each other

I personally would not use the term " magnetic and electric forces eventually balance each other ", because according to Lorentz force, the force on unit charge is $~F=vB ~$ , therefore, according to the definition of electric field, the equivalent electric field felt by the change inside the conductor just happens to be $~E=vB~$.

and then assume that the electric field has this constant value in the left and right segments

As mentioned above, this is not an assumption. Since the moving speed and magnetic field at any point in the vertical segment is the same, the equivalent electric field at any vertical position is also the same. But please note that this concept of so-called equivalent electric field is used to generate EMF for the circuit, it is not necessarily represent the final distribution of electric field and potential difference of the circuit.

But if the electric fields don't have the same value then the amount of charge that is separated must be different too (which is what I was trying to show with my charge separation diagram in my original post). If the amount of charge is different then there will necessarily be some electric field in the top and bottom wires too,

I agree with this statement.

but then this would change the overall EMF in the loop.

Of course everything is related to each other.

How exactly are the charges separated to achieve constant electric fields in the left and right wire segments

This is a very good question. It is not easy to accurately determine the surface charge distribution around the wires in the circuit. However, Ohm's law allows us to easily calculate the voltage drop of each wire in the circuit, so we can also calculate the electric field strength inside each wire in turn.

http://sina.sharif.edu/~aborji/25733/files/Energy transfer in electrical circuits.pdf

 

[Rolls With Slipping]

The electric field from charge separation is conservative so its integral around a closed loop is always zero. The motional EMF in your example is not the integral $\oint \vec{E}\cdot d\vec{l}$ which is zero, it is rather the integral $\oint (\vec{v}\times\vec{B})\cdot d\vec{l}$ around the same loop which is not zero. The difference between those two comes from the top and bottom segments where the $\int_{top} \vec{E}\cdot d\vec{l}\neq 0$ but $\int_{top}(\vec{v}\times\vec{B})\cdot d\vec{l}=0$ (and similar for the bottom wire).

Hmm, I'm not quite following this. There is a charge separation in the wire, right? In your post #4, you discuss the different components of the electric field generated by the charge separation which would be a Coulomb electric field. The current in the long wire is constant and so the magnetic field is constant so there shouldn't be a non-Coulomb electric field generated. Unless there is both a Coulomb and non-Coulomb electric field to consider?

 

[Delta2]

Hmm, I'm not quite following this. There is a charge separation in the wire, right? In your post #4, you discuss the different components of the electric field generated by the charge separation which would be a Coulomb electric field. The current in the long wire is constant and so the magnetic field is constant so there shouldn't be a non-Coulomb electric field generated. Unless there is both a Coulomb and non-Coulomb electric field to consider?

No there isn't any non-Coulomb (non-conservative) electric field to consider. The $\vec{v}\times \vec{B}$ is not conservative (if that's what you mean) but it does not correspond to a non-conservative electric field. It corresponds to the magnetic lorentz force that is responsible for the charge separation.

 

[Delta2]

The EMF around a closed loop is defined as $$\oint (\vec{E}+\vec{v}\times\vec{B})\cdot d\vec{l}=\oint \vec{E}\cdot d\vec{l}+\oint (\vec{v}\times\vec{B})\cdot d\vec{l}$$.
So it consists of two terms. The first term $\oint \vec{E}\cdot d\vec{l}$ if not zero is the transformer EMF and if we have it it means that there is a non-conservative E-field. The second term is the motional EMF, it does not imply by itself the presence of conservative or non-conservative E-fields, however in order to measure it we need a conducting loop in which there will be charge separation and a corresponding coulomb (conservative) E-field.

 

[Rolls With Slipping]

As mentioned above, this is not an assumption. Since the moving speed and magnetic field at any point in the vertical segment is the same, the equivalent electric field at any vertical position is also the same. But please note that this concept of so-called equivalent electric field is used to generate EMF for the circuit, it is not necessarily represent the final distribution of electric field and potential difference of the circuit.

This is a very good question. It is not easy to accurately determine the surface charge distribution around the wires in the circuit. However, Ohm's law allows us to easily calculate the voltage drop of each wire in the circuit, so we can also calculate the electric field strength inside each wire in turn.

http://sina.sharif.edu/~aborji/25733/files/Energy transfer in electrical circuits.pdf

Ok, I think I'm understanding what's going on? The actual distribution of charge in the circuit is rather complicated. Instead of trying to calculate the EMF from this complicated charge distribution, an equivalent electric field is constructed for calculational simplicity.

What this equivalent charge distribution must do is to generate an electric field which is constant in the vertical wire segments. The value of the electric field generated by this charge distribution in the vertical wire segments is such that $E = vB$, $B$ being the value of the magnetic field where each vertical wire segment is located. Further, this equivalent charge distribution also makes the net electric field in the top and bottom wire segments zero.

If you actually went and measured the actual voltage across the vertical wire segments you would probably not get the same value from this simplified picture, but the equivalent current would be the same since the overall EMF generated actually and in this simplified picture is the same.

 

[Rolls With Slipping]

The EMF around a closed loop is defined as $$\oint (\vec{E}+\vec{v}\times\vec{B})\cdot d\vec{l}=\oint \vec{E}\cdot d\vec{l}+\oint (\vec{v}\times\vec{B})\cdot d\vec{l}$$.
So it consists of two terms. The first term $\oint \vec{E}\cdot d\vec{l}$ if not zero is the transformer EMF and if we have it it means that there is a non-conservative E-field. The second term is the motional EMF, it does not imply by itself the presence of conservative or non-conservative E-fields, however in order to measure it we need a conducting loop in which there will be charge separation and a corresponding coulomb (conservative) E-field.

This makes much more sense now. I did not realize this was the complete EMF around a loop. I was only thinking about the first term and conservative/non-conservative electric fields.

So for the case I'm discussing even though there are induced electric fields from this charge separation, it does not contribute to the overall EMF in the loop since these electric fields are due to the charge distribution and not from a time varying magnetic field.

The correct analysis would be that $\oint \vec{E}\cdot d\vec{l} = 0$ and $\oint (\vec{v}\times\vec{B})\cdot d\vec{l} = \int vB_{right} dl - \int vB_{left} dl = Hv(B_{right} - B_{left})$. Which is the same as my result from post #7.

The electric field is irrelevant (at least in calculating in the EMF) since it doesn't contribute to the EMF around the entire loop. I was fixating on the wrong thing!

 

[Delta2]

The electric field is irrelevant (at least in calculating in the EMF) since it doesn't contribute to the EMF around the entire loop. I was fixating on the wrong thing

That's correct but whenever we have motional EMF only, in which case they appear only conservative E-fields around a conducting loop. In case that we have transformer EMF there is a non-conservative electric field (due to the time varying magnetic field) and which contributes to the total EMF.

 

[alan123hk]

The value of the electric field generated by this charge distribution in the vertical wire segments is such that E=vB, B being the value of the magnetic field where each vertical wire segment is located. Further, this equivalent charge distribution also makes the net electric field in the top and bottom wire segments zero.

The Lorentz forces acting on the upper and lower horizontal segments are vertical, so they do not contribute to the calculation of the loop current. But in fact, as long as the two horizontal segments have non-zero resistance, they will each have their own potential difference $~V=IR~$, where I=loop current and R=resistance, and the potential difference means that there is an electric field in the horizontal direction.

 

[alan123hk]

Let's try a simple calculation example.

Right vertical segment : EMF₁ due to $~vBl~$ = 2V ; R₁ = 4 ohm
Left vertical segment : EMF₂ due to $~vBl~$ = 1V ; R₃ = 3 ohm
Upper horizontal segment : R₂ = 2 ohm
Lower horizontal segment : R₄ = 1 ohm
The length of the 4 segments is the same = 1 meter

Loop current : I_c = (EMF1-EMF2)/(R1+R2+R3+R4)=0.1A

Potential difference of the right vertical segment : $~V_1 =EMF_1-I_c R_1= 1.6~V$
Potential difference of the left vertical segment : $~V_3 =-EMF_2-I_c R_3=-1.3~V$
Potential difference of the upper horizontal segment : $~V_2 =-I_c R_2=-0.2~V$
Potential difference of the lower horizontal segment : $~V_4 =-I_c R_4=-0.1~V$

The total voltage around the loop = V₁ + V₂ + V₃ + V₄ = 1.6 - 0.2 - 1.3 - 0.1 = 0, so this satisfied the Kirchhoffs Voltage Law.

If we assume that the resistivity of all segments does not change with their position in the corresponding segment, the electric fields in the segments will be

E₁ (point down) = 1.6V/m,
E₂ (point to left) = 0.2V/m,
E₃ (point down)=1.3V/m,
E₄ (point to right) =0.1V/m,
respectively.

Note that, for example, the right vertical segment EMF₁=2V, but the corresponding potential difference is actually just 1.6V.

I hope I didn't get something wrong.

PS. As for the precise charge distribution, this is a very difficult problem, which may be beyond my ability.

 

[Rolls With Slipping]

The Lorentz forces acting on the upper and lower horizontal segments are vertical, so they do not contribute to the calculation of the loop current. But in fact, as long as the two horizontal segments have non-zero resistance, they will each have their own potential difference $~V=IR~$, where I=loop current and R=resistance, and the potential difference means that there is an electric field in the horizontal direction.

Right, of course! If there is a current and resistance in a wire segment it will necessarily have a voltage care of Ohm's law meaning there will be an electric field in the top and bottom segments. Got it!

 

[Rolls With Slipping]

Note that, for example, the right vertical segment EMF₁=2V, but the corresponding potential difference is actually just 1.6V.

I hope I didn't get something wrong.

This seems fine. A real battery for example has an internal resistance meaning the actual voltage across its terminals is less than its ideal voltage. If you think of the vertical segments as "batteries" then the EMF would be the ideal voltage and the resistance of the wire is the internal resistance of the equivalent real battery.