Electric Potential Homework: Find VA & VB

[zorro]

Homework Statement

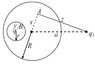
A cavity is made inside a solid conducting sphere and a charge q is placed inside the cavity at the centre. A charge q1 is placed outside the sphere as shown in the figure. Point A is inside the sphere and point B is inside the cavity. Find potential at A and B.

[URL]http://203.196.176.41/VLEBT_RootRepository/Resources/5cef7d9a-41c3-4283-bf26-9a89c8369923.jpg[/URL]

The Attempt at a Solution

The problem I have here is the effect of outer charge on the potential. There will be an induced charge -q1 on the sphere due to it. So the potential due to -q1 is -kq1/R.
There will be induced charge of q on the outer surface of the bigger sphere, so potential due to it at A=kq/R

VA= -kq1/R + kq/R

Is it fine? How do I calculate V at B? I am a bit confused here.

 

[supratim1]

let surface of sphere get effective charge Q.

so Q = -q1 + q

So VA = same as you calculated.

and VB = -kq1/r

 

[zorro]

Sorry your answer is wrong.

 

[supratim1]

what is the correct answer then?

 

[SammyS]

A figure would help us help you.

Have you studied image charges?

You are correct that q₁ will induce a charge on the surface of the sphere, however, it will not be uniformly distributed on the surface, in fact, the net charge induced by q₁ is zero. Superimposed on the surface is a uniformly distributed charge of q plus the charge induced by q₁.

 

[zorro]

@Supratim
I won't tell that. You figure out yourself.

@SammyS
No I did not study image charges.
What is the charge induced by q1 on the surface? Isn't it equal to -q1?
Can you explain an easy method to find out the potential at B?

 

[SammyS]

@SammyS
No I did not study image charges.
What is the charge induced by q1 on the surface? Isn't it equal to -q1?
Can you explain an easy method to find out the potential at B?

If the sphere was grounded (Earthed) when q₁ was brought to position, then q₁ would induce a charge on the sphere, the magnitude of the induced charge being less the q₁. It would be just enough so that if you would replace the sphere with a point charge equal to the induced charge, there would be a spherical equi-potential surface at the location previously occupied by the sphere. (The location of this point charge would not be at the center of the sphere it replaced.)

Assuming the sphere is isolated when q₁ is brought into place, q₁ can not change the net charge on the sphere, only the charge distribution. The presence of q₁ does affect the potential of the sphere.

Without more details, including some which might be provided in the figure mentioned in the Original Post, I am limited in how much I can help.

Assuming the radius of the sphere is R, I can make the following comments:

1. The potential V_A at point A is the same as the potential at any other place in the conducting material of the sphere.

2. The potential difference, V_B ‒ V_sphere = kq/R_B ‒ kq/R_cavity

3. The net charge on the surface of the sphere is q. The net charge on the surface of the cavity is ‒q.​

What is the location of q₁ relative to the sphere?

 

[zorro]

2. The potential difference, V_B ‒ V_sphere = kq/R_B ‒ kq/R_cavity

If we ignore the outer charge q1 for a moment, I calculated the potential at B=

kq/R - (kq/y - kq/r)
[Potential at B due to sphere without cavity - Potential at B due to a sphere that fits in the cavity]
How do I find the potential due to the outer charge q1 alone?

What is the location of q₁ relative to the sphere?

It is at a distance 'a' from the centre of the sphere.

 

[SammyS]

This requires using the principle of superposition to "build up" a solution.

Place the sphere, radius R, so its center is at the origin. Place charge q₁ on the x-axis at x=a, a>R. Now let's see if we can replace the sphere with a charge of q₂ located at x = p on the positive x-axis at the proper location, and with the proper charge to make the potential zero at r = R, i.e. at x² + y² + z² = R², the place where the surface of the sphere was located.

We'll just work at x = ±R. That will give two equations in two unknowns.

At x = R we have  V=\frac{kq_1}{a-R}+\frac{kq_2}{R-p}=0\,.\quad\to\quad\frac{q_1}{a(1-\frac{R}{a})}+\frac{q_2}{R(1-\frac{p}{R})}=0

At x = ‒R we have  V=\frac{kq_1}{a+R}+\frac{kq_2}{R+p}=0\,.\quad\to\quad\frac{q_1}{a(1+\frac{R}{a})}+\frac{q_2}{R(1+\frac{p}{R})}=0

By inspection, both equations will work if:

\frac{q_1}{a}=\frac{q_2}{R}\quad\text{And}\quad\frac{R}{a}=\frac{p}{R}

For fun, verify that this makes the potential zero whenever x² + y² = R².

 

[zorro]

This requires using the principle of superposition to "build up" a solution.

Place the sphere, radius R, so its center is at the origin. Place charge q₁ on the x-axis at x=a, a>R. Now let's see if we can replace the sphere with a charge of q₂ located at x = p on the positive x-axis at the proper location, and with the proper charge to make the potential zero at r = R, i.e. at x² + y² + z² = R², the place where the surface of the sphere was located.

We'll just work at x = ±R. That will give two equations in two unknowns.

At x = R we have  V=\frac{kq_1}{a-R}+\frac{kq_2}{R-p}=0\,.\quad\to\quad\frac{q_1}{a(1-\frac{R}{a})}+\frac{q_2}{R(1-\frac{p}{R})}=0

At x = ‒R we have  V=\frac{kq_1}{a+R}+\frac{kq_2}{R+p}=0\,.\quad\to\quad\frac{q_1}{a(1+\frac{R}{a})}+\frac{q_2}{R(1+\frac{p}{R})}=0

By inspection, both equations will work if:

\frac{q_1}{a}=\frac{q_2}{R}\quad\text{And}\quad\frac{R}{a}=\frac{p}{R}

For fun, verify that this makes the potential zero whenever x² + y² = R².

Damn! the link I provided for the image was from a temporary site (stored in my mozilla cookies). When I restarted my laptop it vanished!
I did not read your post #5 properly, sorry for the inconvenience

I got q₂= -q₁R/a

I calculated the potential due to q1 and q2 and found them to be equal to -kq₁/R + kq₁/a (assuming that the point B inside the cavity is inside the sphere formed with radius 'p').
Thank you for teaching me about image charges

 

[SammyS]

Damn! the link I provided for the image was from a temporary site (stored in my mozilla cookies). When I restarted my laptop it vanished!
I did not read your post #5 properly, sorry for the inconvenience

It happens. I've been fooled by posting an image that I could see, then having it disappear.

I got q₂= -q₁R/a

I calculated the potential due to q1 and q2 and found them to be equal to -kq₁/R + kq₁/a (assuming that the point B inside the cavity is inside the sphere formed with radius 'p').
Thank you for teaching me about image charges

I assume the sphere isn't grounded, but at any rate, a net charge of q₂ = -q₁R/a on the sphere will produce a Potential of 0 (the same as at infinity) at the outer surface of the sphere (r=R).

To find the potential of the the sphere having a charge of q on its surface, use the DIFFERENCE: q - q₂ = q + q₁R/a on a sphere of radius R.

Got to go ! Later ...

 

[zorro]

The image reappeared in my laptop today.
I am attaching it.

To find the potential of the the sphere having a charge of q on its surface, use the DIFFERENCE: q - q2 = q + q1R/a on a sphere of radius R.

I did not get your point here.

In the figure,
V at B = kq/R - (kq/y - kq/r) -kq1/R + kq1/a

Is this not right?

 

[SammyS]

The image reappeared in my laptop today.
I am attaching it.

I did not get your point here.

In the figure,
V at B = kq/R - (kq/y - kq/r) -kq1/R + kq1/a

Is this not right?

(Sorry about not replying sooner.)

Not right.

The conducting sphere is all at one potential, because the E field is zero everywhere within the conducting material.

The potential at point B minus the potential of the sphere is: V_B ‒ V_sphere = kq/y ‒ kq/r .

All that's needed beyond this is to find the potential of the sphere.

 

[SammyS]

...
I got q₂= -q₁R/a

I calculated the potential due to q1 and q2 and found them to be equal to -kq₁/R + kq₁/a (assuming that the point B inside the cavity is inside the sphere formed with radius 'p').
Thank you for teaching me about image charges

The q₂ = ‒q₁R/a is correct. (You corrected my sign error.)

Your interpretation isn't quite right.

Let's build up a solution using superposition:

A charge of -q₁R/a at x = p, where p = R²/a and a charge of q₁ at x=a, will produce a potential of zero a distance of R from the origin -- that is the location of the surface of a sphere of radius R centered at the origin.

We could replace a grounded sphere (radius R, center @ origin) with this image charge. The electric potential and the E field would match everywhere beyond a distance of R from the origin, for either configuration.​

... but we don't have a grounded sphere.

That brings us to the next step:

Start with a neutral conducting sphere (radius R, center @ origin), bring a charge of q₁ from ∞ to x = a. This sphere is NOT grounded ! We could replace the sphere with our image charge, q₂ = ‒q₁R/a at x = R²/a , plus a charge of ‒q₂ = +q₁R/a @ the origin, in addition to the charge q₁ @ x = a. But think about it! ... q₂ @ x = p and q₁ @ x = a give us a potential of zero @ a distance of R from the origin, ...

so, simply use a charge of q₁R/a at the origin --- to find what the potential of a neutral conducting sphere of radius R, center @ origin.

However, our sphere has a net charge of q on it's exterior, so to find the potential at it's surface, find the potential @ a distance of R from the origin, due to a charge of q + ‒q₂ = q + q₁R/a all situated at the origin.

This gives the potential of all of the conducting sphere including all the way down to the surface of the cavity in it.​

 

[zorro]

simply use a charge of q1R/a at the origin --- to find what the potential of a neutral conducting sphere of radius R, center @ origin.

So we can remove the outer charge q1 and replace it with a charge of q1R/a at the origin, right?

However, our sphere has a net charge of q on it's exterior, so to find the potential at it's surface, find the potential @ a distance of R from the origin, due to a charge of q + ‒q₂ = q + q₁R/a all situated at the origin.

This gives the potential of all of the conducting sphere including all the way down to the surface of the cavity in it.​

I don't understand why you are subtracting q₂ from q. Why don't we add them?

 

[SammyS]

So we can remove the outer charge q1 and replace it with a charge of q1R/a at the origin, right?

I don't understand why you are subtracting q₂ from q. Why don't we add them?

(The following is prior to taking into account the presence of charge q in the cavity.)

IF the sphere were at zero potential (grounded), then bringing charge q₁ into place would induce a charge of q₂ = -q₁R/a on the sphere.
BUT, the sphere is neutral & it's not grounded. In this case, charge q₁ changes the distribution of charge on the surface of the sphere, but it can't add or remove charge. We can model this as the superposition of two spheres (at the same location). One has charge q₂ distributed in such a way that it produces an E field identical to what the equivalent image charge would produce. The 2nd sphere to be superimposed must have a charge equal in magnitude & opposite in sign to q₂, so this second charge is -q₂. It is uniformly distributed over the surface of the conducting sphere. Keep in mind that -q₂ = +q₁R/a .

Since the image charge merely gives zero potential at the surface of the sphere, all you need is the charge -q₂ = q₁R/a. NOW add to this the charge of q, also distributed uniformly over the surface of the sphere. These will give you the potential of the sphere.

 

[zorro]

I understood everything perfectly now.
1 question - Will the potential due to q + q₁R/a be constant inside the cavity too? i.e. will it be equal to kq/R + kq₁/a ? If yes then why?

 

[SammyS]

I understood everything perfectly now.
1 question - Will the potential due to q + q₁R/a be constant inside the cavity too? No

i.e. will it be equal to kq/R + kq₁/a ? If yes then why?

Point B is a distance of y from the center of the cavity. The potential difference between Point B and the surface of the cavity is V_B - V_SPHERE = kq/y - kq/r, where r is the radius of the cavity.

V_{B}-V_{sphere}=-\int_{r}^{\,y}\frac{kq}{r^2}\,dr\,.

This is after translating the coordinate system so that the origin is at the center of the cavity.

 

[zorro]

I think you did not get my question (or I did not get you )

Let me write the final analysis-

If we remove the cavity and consider a full sphere (w/o cavity) of radius R with charge q+q₁R/a on it, the potential at point B is kq/R + kq₁/a

Now since there is a cavity with charge q at the centre and -q on its inner surface, potential at B = kq/y - kq/r

So net potential al B = (kq/R + kq₁/a) + (kq/y - kq/r) (by using superposition principle)

 

[SammyS]

I think you did not get my question (or I did not get you )

Let me write the final analysis-

If we remove the cavity and consider a full sphere (w/o cavity) of radius R with charge q+q₁R/a on it, the potential at point B is kq/R + kq₁/a

Now since there is a cavity with charge q at the centre and -q on its inner surface, potential at B = kq/y - kq/r : This is relative to the potential of the sphere.

So net potential al B = (kq/R + kq₁/a) + (kq/y - kq/r) (by using superposition principle) YES!

Sorry, I missed the question.

Yes! I think you've got it!

 

[zorro]

Thanks for bearing with me. Your explanations were very good.
I request PF Admin to award you with a 'Homework Helper' recognition

 

[SammyS]

Thanks!

I sent you a message.