[Electrical force] 2 balls hanging from ceiling, angled

[sea333]

Homework Statement

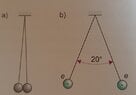
2 metal balls hang from a ceiling on a thread(see picture a.) ). After the balls are charged with the same charge both thread diverge to an angle 20 degrees.(see picture b.) )
What charge is used to charge each ball.
weight of each ball = 0.02 kg

Relevant Equations

F = (1/(4*Pi*eps0))*(e*e)/r^2

 

[kuruman]

Your expression $F_e=mg\tan(10^o)$ is incorrect. The electric force is equal to the horizontal component of the tension, the weight is equal to the vertical component of the tension and $T=\sqrt{(mg)^2+F_e^2}.$

 

[sea333]

Your expression $F_e=mg\tan(10^o)$ is incorrect. The electric force is equal to the horizontal component of the tension, the weight is equal to the vertical component of the tension and $T=\sqrt{(mg)^2+F_e^2}.$

ok but neither the Tension nor Fe are known, and we need Fe ?

 

[kuruman]

Write down two equations balancing forces in the horizontal and vertical directions separately and see where you can go from there.

 

[sea333]

Write down two equations balancing forces in the horizontal and vertical directions separately and see where you can go from there.

horizontal: Fx - Fe = 0 -> Fe = Fx
vertical: Fg - Fy = 0 -> Fg = Fy

 

[kuruman]

horizontal: Fx - Fe = 0 -> Fe = Fx
vertical: Fg - Fy = 0 -> Fg = Fy

This is correct but doesn't get you very far. You need to bring in the given quantities. Please use symbols like m and q and so on, not numbers. The numbers will be substituted in the final expression for q once you have it.

 

[sea333]

This is correct but doesn't get you very far. You need to bring in the given quantities. Please use symbols like m and q and so on, not numbers. The numbers will be substituted in the final expression for q once you have it.

Fe = Fx
Fg = Fy
Fx = (1/(4*PI*Eps0))*(q*q/r^2)
Fy = mg

 

[kuruman]

Right. But you have not brought in the information that the string makes a 10^o angle with respect to the vertical. How would you go about doing that?

 

[sea333]

Right. But you have not brought in the information that the string makes a 10^o angle with respect to the vertical. How would you go about doing that?

that is cosinus -> T = mg / Cos10

 

[kuruman]

Correct. What can you say about the horizontal direction?

 

[sea333]

this
Fx - Fe = 0
Fx = (1/(4*PI*Eps0))*(q*q/r^2)

 

[kuruman]

And how is Fx related to T?

 

[sea333]

Fx/T = sin 10 -> Fx = Fe = T*sin10

 

[kuruman]

OK. You have two equations one in the vertical direction and one in the horizontal direction involving T, mg and the electrical force. Can you write them down, one below the other?

 

[sea333]

T = mg / Cos10
Fx = Fe = T*sin10

 

[kuruman]

How does that help you find q?

 

[sea333]

Into the bottom equitation I can insert equation for T and get q which is the only unknown?

 

[kuruman]

Please show me how you are going to do this.

 

[sea333]

q*q/(4*PI*Eps0*r^2) = (m*g / Cos10) * Sin10

And then just move everything except q on the right side

 

[kuruman]

That sounds about right. You already have r from your initial attempt.

 

[sea333]

This looks easy, but why was my attempt flawed with Tan10 ?

 

[kuruman]

This looks easy, but why was my attempt flawed with Tan10 ?

I explained that in post #2.

 

[haruspex]

This looks easy, but why was my attempt flawed with Tan10 ?

That was fine, but you have a wrong sign in your use of the cosine rule to find r. Easier would have been $r=a\sin(10°)$.

Edit: see correction in post #27.

 

[sea333]

That was fine, but you have a wrong sign in your use of the cosine rule to find r. Easier would have been $r=a\sin(10°)$.

When I changed the sign now result looks correct.
I don't think you can get r in such a way because angle 10 degrees is not adjacent to r

 

[sea333]

I explained that in post #2.

It looks like the Tan approach was correct

 

[sea333]

correct solution

 

[haruspex]

When I changed the sign now result looks correct.
I don't think you can get r in such a way because angle 10 degrees is not adjacent to r

Sorry, I meant $r=2a\sin(10°)$.

 

[sea333]

Sorry, I meant $r=2a\sin(10°)$.

I still don't see how this is correct as angle 10 is not adjacent to r

 

[kuruman]

I still don't see how this is correct as angle 10 is not adjacent to r

You have found that $r=\sqrt{2a^2-2a^2\cos^2(20^o)}=\sqrt{2a^2(1-\cos(20^0))}$.
There is a trig identity that says
$\cos(2\theta)=\cos^2(\theta)-\sin^2(\theta)$
so that $1-\cos(20^0)=1-\cos^2(10^o)+\sin^2(10^o)=2\sin^2(10^o)$. What do you get when you substitute in the expression for $r$?

Another way to look at it is to break the isosceles triangle to two right triangles of base $r/2$ and hypotenuse $a$. How is $r/2$ related to $a$?

 

[sea333]

sqrt(4a^2sin^2(10)) = 2*a*sin10

How do you get from 1 - cos^2(10) - sin^2(10) to 2 sin^2(10) ?