- #1
Bound
- 9
- 0
Some background: This was a quiz I recently had in which I lost a few points for missing an "x & y component" for one of the directions.
My thinking is that because the problem was not actually set up with a specified order of charges there are a few different answers you could get.
I intend to bring this up with the teacher, but thought I'd see what you guys have to say as well.
Three charges are arranged in the shape of an equilateral triangle. (Note- no diagram is given)
The charge magnitudes are as follows:
q1=+4*10-6C, q2=-6.5*10-6C, q3=+2.1*10-6C
The distance between each charge is 2m
Calculate the electric force on q3.
F = (kq1q2) / d2
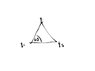
I set my triangle up as: (see attached picture)
Calculated force of 1 on 3:
F = .0189 N
X-component of F13:
Fx=(.0189)(sin30)
=.00945 N
Y-component of F13:
Fy=(.0189)(cos30)
=.0163676801 N
*Marked Correct*
Calculated force of 2 on 3:
F = -.0307125 N
*Marked incorrect for not separating into x & y components*
Would this not be correct though? The way I set my triangle up has 2 on a straight horizontal line across from 3!
My further work is just adding up all of the components of everything for a final answer of:
Net Force on q3 = .0268 N @ 37.6deg SofW
Thanks for any help!
My thinking is that because the problem was not actually set up with a specified order of charges there are a few different answers you could get.
I intend to bring this up with the teacher, but thought I'd see what you guys have to say as well.
Homework Statement
Three charges are arranged in the shape of an equilateral triangle. (Note- no diagram is given)
The charge magnitudes are as follows:
q1=+4*10-6C, q2=-6.5*10-6C, q3=+2.1*10-6C
The distance between each charge is 2m
Calculate the electric force on q3.
Homework Equations
F = (kq1q2) / d2
The Attempt at a Solution
I set my triangle up as: (see attached picture)
Calculated force of 1 on 3:
F = .0189 N
X-component of F13:
Fx=(.0189)(sin30)
=.00945 N
Y-component of F13:
Fy=(.0189)(cos30)
=.0163676801 N
*Marked Correct*
Calculated force of 2 on 3:
F = -.0307125 N
*Marked incorrect for not separating into x & y components*
Would this not be correct though? The way I set my triangle up has 2 on a straight horizontal line across from 3!
My further work is just adding up all of the components of everything for a final answer of:
Net Force on q3 = .0268 N @ 37.6deg SofW
Thanks for any help!
Attachments
Last edited: