- #1
elephantorz
- 35
- 0
1.
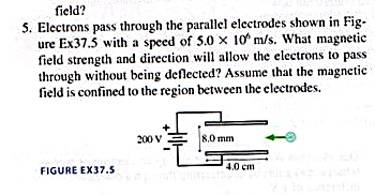
2. Homework Equations : are too big to post here, meaning, I will give you a link to my work:
http://farm4.static.flickr.com/3092/2369876018_5866bfb312_o.jpg"
3. The Attempt at a Solution : that's above as well, I know what the solution IS, it's at the top righthand corner of the page, boxed in.
I have been looking everywhere for homework help, since I'm doing independent study and my teacher is not always available (it's Spring Break, neither are the tutors).
I'm doing special relativity so far, and now I'm looking at electrons and positrons, parallel capacitors, etc. I have issues specifically with the easy stuff (for some reason I get the hard stuff just fine...).
If you can't read the problem above it let me know I will transcribe it, now, I have worked out that somehow, thanks to the book's example, I have to set up a right triangle. As you can see by my work (ignore the top figurings, that's just me setting up, what you want to look at are the formulas and the stuff that's worked out fully at the end of the page; also I know it's E instead of B in the last equation there, I think I was losing it by that time).
I don't know what I am doing wrong because I am lost in one sense and the book is unhelpful, I just want to understand it so I can move on to other things and other problems, btw this site rules :D.
2. Homework Equations : are too big to post here, meaning, I will give you a link to my work:
http://farm4.static.flickr.com/3092/2369876018_5866bfb312_o.jpg"
3. The Attempt at a Solution : that's above as well, I know what the solution IS, it's at the top righthand corner of the page, boxed in.
I have been looking everywhere for homework help, since I'm doing independent study and my teacher is not always available (it's Spring Break, neither are the tutors).
I'm doing special relativity so far, and now I'm looking at electrons and positrons, parallel capacitors, etc. I have issues specifically with the easy stuff (for some reason I get the hard stuff just fine...).
If you can't read the problem above it let me know I will transcribe it, now, I have worked out that somehow, thanks to the book's example, I have to set up a right triangle. As you can see by my work (ignore the top figurings, that's just me setting up, what you want to look at are the formulas and the stuff that's worked out fully at the end of the page; also I know it's E instead of B in the last equation there, I think I was losing it by that time).
I don't know what I am doing wrong because I am lost in one sense and the book is unhelpful, I just want to understand it so I can move on to other things and other problems, btw this site rules :D.
Last edited by a moderator: