Spathi
Gold Member
- 102
- 10
- TL;DR
- When a photon passes through the first semi-transparent mirror, it turns into a superposition of photons traveling along the upper and lower paths. In MMI this means that two "parallel worlds" appear...
https://en.wikipedia.org/wiki/Elitzur–Vaidman_bomb_tester
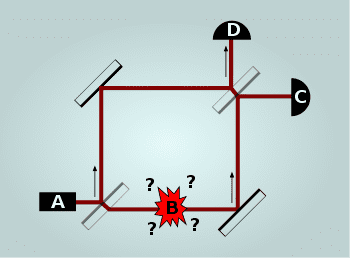
In the Elitztur-Weidman experiment there are bombs that are triggered by a single photon hitting their detector, and with some probability you can find out that the bomb is working, despite the fact that it did not explode.
I'm trying to formulate how this experiment can be described in the many-worlds interpretation. When a photon passes through the first semi-transparent mirror, it turns into a superposition of photons traveling along the upper and lower paths. In MMI this means that two parallel worlds appear (I do not like the word "parallel" but there is no other yet), in the first one the photon goes along the upper path, in the second - along the lower one. In the first world the photon hits detector D or C, in the second it is absorbed by the bomb and the detectors see nothing. Yet it didn't become clearer; probably, in order to move forward, you need to figure out what happens to the photon or superposition on the second semitransparent mirror. It is written that the superposition interferes with itself and is detected in C; what is the correct name for the reverse transformation of a superposition into a single reality - decoherence or destructive interference?
In the Copenhagen interpretation, the experiment can be stated as follows. The bomb is an observer, the hit of a photon on its detector is a measurement process, i.e. wave function collapse. As a result of the collapse, the superposition turns into a single photon flying either along the lower path or along the upper one. If on the top - it is detected on D and so we find out that the bomb worked. If I'm not confused, Wikipedia says that if a superposition of photons hits the second mirror, then it decoheres and a photon is always detected at C; if a photon flying along the upper path hits, then it is reflected and detected either on C or on D. I did not find in the article what will happen if the photon passes only through the lower path. Maybe we are talking about the fact that this is impossible - if the bomb is faulty, then there will always be only a superposition?
It is still unclear to me how such an experiment is possible from a technical point of view. In order for the superposition of two photons to merge again into one photon, is it necessary that the first and second components of the superposition meet exactly at a single point in space? I mean that if, for example, in this setting, the length of the horizontal path is increased by one and a half times, and the length of the vertical path is not changed, then the superposition will not merge on the second translucent mirror, because the top and bottom photon will not meet in the same place? Then it turns out that for a correct experiment it is necessary to adjust the geometrical parameters of the installation to within an atom, very strange.
Just in case, I will state, as it is written in Wikipedia: if the bomb is in good condition, with a probability of 50% the photon will not be detected (the bomb exploded), with a probability of 25% it will be detected on C (as I understand it, the bomb also exploded) and with a probability of 25% it will be detected on D (the bomb is working but did not explode).
In the Elitztur-Weidman experiment there are bombs that are triggered by a single photon hitting their detector, and with some probability you can find out that the bomb is working, despite the fact that it did not explode.
I'm trying to formulate how this experiment can be described in the many-worlds interpretation. When a photon passes through the first semi-transparent mirror, it turns into a superposition of photons traveling along the upper and lower paths. In MMI this means that two parallel worlds appear (I do not like the word "parallel" but there is no other yet), in the first one the photon goes along the upper path, in the second - along the lower one. In the first world the photon hits detector D or C, in the second it is absorbed by the bomb and the detectors see nothing. Yet it didn't become clearer; probably, in order to move forward, you need to figure out what happens to the photon or superposition on the second semitransparent mirror. It is written that the superposition interferes with itself and is detected in C; what is the correct name for the reverse transformation of a superposition into a single reality - decoherence or destructive interference?
In the Copenhagen interpretation, the experiment can be stated as follows. The bomb is an observer, the hit of a photon on its detector is a measurement process, i.e. wave function collapse. As a result of the collapse, the superposition turns into a single photon flying either along the lower path or along the upper one. If on the top - it is detected on D and so we find out that the bomb worked. If I'm not confused, Wikipedia says that if a superposition of photons hits the second mirror, then it decoheres and a photon is always detected at C; if a photon flying along the upper path hits, then it is reflected and detected either on C or on D. I did not find in the article what will happen if the photon passes only through the lower path. Maybe we are talking about the fact that this is impossible - if the bomb is faulty, then there will always be only a superposition?
It is still unclear to me how such an experiment is possible from a technical point of view. In order for the superposition of two photons to merge again into one photon, is it necessary that the first and second components of the superposition meet exactly at a single point in space? I mean that if, for example, in this setting, the length of the horizontal path is increased by one and a half times, and the length of the vertical path is not changed, then the superposition will not merge on the second translucent mirror, because the top and bottom photon will not meet in the same place? Then it turns out that for a correct experiment it is necessary to adjust the geometrical parameters of the installation to within an atom, very strange.
Just in case, I will state, as it is written in Wikipedia: if the bomb is in good condition, with a probability of 50% the photon will not be detected (the bomb exploded), with a probability of 25% it will be detected on C (as I understand it, the bomb also exploded) and with a probability of 25% it will be detected on D (the bomb is working but did not explode).