Elongation of a bar problem | Timoshenko

[newbie1127]

Homework Statement

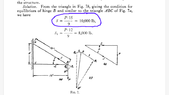
Determine the cross-sectional dimensions of the wooden beam BC and of the steel bar AB of the structure ABC, loaded at B, if the workin stress for pine wood is taken as crw = 160 lb per sq in. and for steel a~ = 10,000 lb per sq in. The load P = 6,000 lb. The dimensions of the structure are shown in Fig. 7. Determine the vertical and the horizontal components of the displacement of the point B due to deformation of the bars. Neglect the weight of the structure.

Relevant Equations

d(Change in length) = (Load x Length) / (E x Area)

hi everyone,

In a problem where we have to find the change in length of a steel bar and a wooden beam,
while calculating the change in length the author multiplied the entire thing by 12

I put all the values in the above equation and still couldn't account for the 12.

Thinking of it nothing more than a print mistake i moved on, only later to find the same thing in the same type of problem.
I'll put all the values down below to paint a more detailed picture:

Length of bar = 15 inch
Tension on bar = 10000 lb
E = 30 x 10^6 lb/sq.in
A = 1 sq.in

After putting all these in the equation, the answer comes out to be 0.005 inch. However, the author has answer as 0.060 inch, differeing by a magnitude of 12x

I don't know why it is like that. help please

some reference :

the figure and solution offered by author - I'll attach a screenshot of these

 

[Baluncore]

Where does the problem come from?
Maybe the original bar length was 15 feet, but has now been changed to 15 inches, and the answer did not have the 12 inches per foot conversion removed.

 

[newbie1127]

Where does the problem come from?
Maybe the original bar length was 15 feet, but has now been changed to 15 inches, and the answer did not have the 12 inches per foot conversion removed.

you're right Mr.baluncore, it is the problem, thanks :)

 

[Baluncore]

I see your problem on page 11. You are not the first to read it that way.
Now you know the advantage of using the MKSA international system of units.

 

[newbie1127]

I see your problem on page 11. You are not the first to read it that way.
Now you know the advantage of using the MKSA international system of units.

thanks for not roasting me.
i also prefer the SI system, but i could only find this book in the inch system.