phantomvommand
- 287
- 39
- Homework Statement
- Please see attached photos.
- Relevant Equations
- Ampere's Law
The task is to find the magnetic field between the 2 long cylinders, which extend to infinity. Integration is involved to find the total current passing through the Amperian Loop shown below. What I do not understand is why only sides 1 and 3 contribute to that B ds part of Ampere's Law. Isn't there magnetic field flowing parallel to sides 2 and 4 as well, like how a current in a straight wire creates a circular magnetic field that runs parallel to all sides of a loop around it?
I see this as similar to a straight wire, as there is only an X-component of current. The Y-component cancels out. However, there is "thickness" to this current.
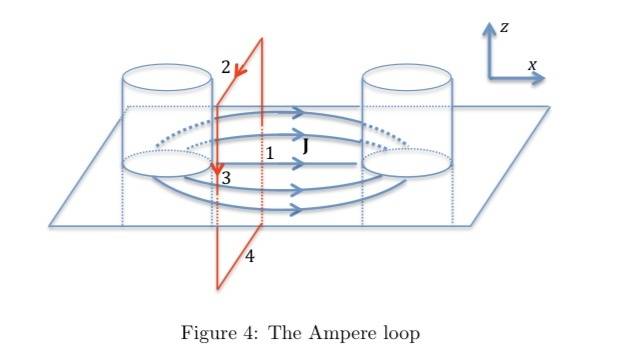
I see this as similar to a straight wire, as there is only an X-component of current. The Y-component cancels out. However, there is "thickness" to this current.
Last edited by a moderator: