- #1
twiztidmxcn
- 43
- 0
These circuit questions seem to give me so many problems, this question in particular.
What are the emf and internal resistance of the battery in the figure below?
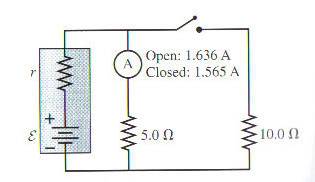
I have the answers, that emf is 9V and internal resistance is 0.5 ohms, however I'm having problems getting there.
What I did was first treat the two outside resistors as being in parallel and found their equivalent resistance
1 / R eq = 1 / R1 + 1 / R2 = 1/5 + 1/10, Req = 10/3
So then the internal resistance and that new Req are in series, so Req = r + 10/3 ohms.
Now, I come to my problem. I assumed that when the switch is open, all the current is running through the ammeter and the 5ohm resistor. Using V=IR, I solved for V and found it to be 7.825. Knowing that resistors in parallel have the same voltage, i knew that V1 = V2, so I1R1=I2R2, solved for I2 and found it to be 0.7825A.
Now having a current and the resistance of the outside resistor, i know that I = emf / R + r. I am stuck as to where to go now, how to find emf and r.
I also know that V = emf - IR. I tried to use this equation and the one above to solve down for emf or r using systems of equations but continually find myself cancelling both out with nothing to solve for. yes, it turns out emf does = emf.
Any help in the right direction would be awesome
thx
twiztidmxcn
What are the emf and internal resistance of the battery in the figure below?
I have the answers, that emf is 9V and internal resistance is 0.5 ohms, however I'm having problems getting there.
What I did was first treat the two outside resistors as being in parallel and found their equivalent resistance
1 / R eq = 1 / R1 + 1 / R2 = 1/5 + 1/10, Req = 10/3
So then the internal resistance and that new Req are in series, so Req = r + 10/3 ohms.
Now, I come to my problem. I assumed that when the switch is open, all the current is running through the ammeter and the 5ohm resistor. Using V=IR, I solved for V and found it to be 7.825. Knowing that resistors in parallel have the same voltage, i knew that V1 = V2, so I1R1=I2R2, solved for I2 and found it to be 0.7825A.
Now having a current and the resistance of the outside resistor, i know that I = emf / R + r. I am stuck as to where to go now, how to find emf and r.
I also know that V = emf - IR. I tried to use this equation and the one above to solve down for emf or r using systems of equations but continually find myself cancelling both out with nothing to solve for. yes, it turns out emf does = emf.
Any help in the right direction would be awesome
thx
twiztidmxcn