Empirical tight-binding sp3s* band structure of semiconductors

[rogdal]

TL;DR Summary

I'm looking for the spin-orbit splitting parameters of certain semiconductors at T = 0 K and their dependance on temperature.

I'm simulating on code the tight-binding sp3s* bandstructure of certain semiconductors, such as GaAs, AlP, InP, ZnSe, etc. with spin-orbit coupling at a temperature of T = 0 K but I'm having trouble at finding the corresponding spin-orbit splitting parameters.

For example, I've found in this article by Vogl et al, A Semi-Empricial Tight-Binding Theory of the Electronic Structure of Semiconductors the following relation of spin-orbit parameters:

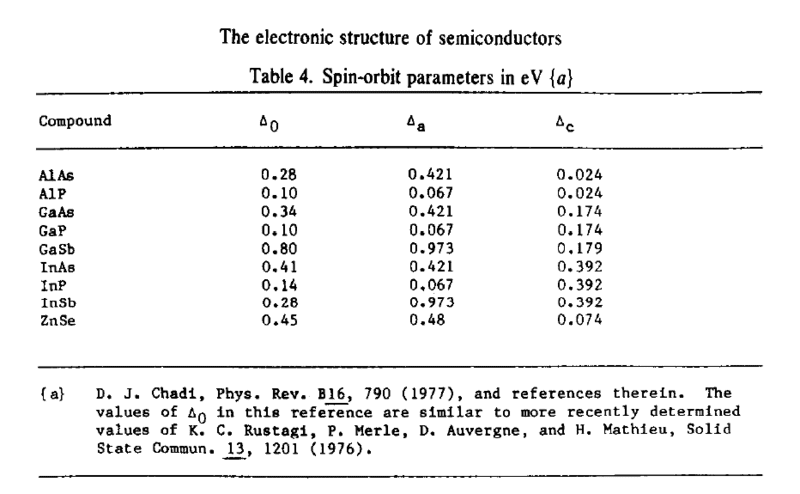
But the temperature is not said anywhere in that article. In fact, the tight binding parameters without spin-orbit coupling depend a lot on the temperature. At this point, the only information that is certain for me is the following:

1) At T = 300 K the desired parameters appear in this article by Klimeck et al: sp3s* Tight-binding parameters for transport simulations in compound semiconductors

2) At T = 0 K I know from chapter 5 of Supriro Datta's Quantum Transport, Atom to Transistor that the spin-orbit parameters, only for GaAs are D_a = 0.37 eV for Arsenic and D_c = 0.013 eV for Gallium. The other semiconductors are not mentioned.

Based on what I've said above, do you know where I could find the spin-orbit splitting parameters for the semiconductors on Table 4 at T = 0 K, and if it were possible their dependance with the temperature? Any references will be appreciated.

Thank you very much!

 

[Dr Transport]

They will be fairly accurate at low T, since that is where the measurements were probably made.

 

[rogdal]

Thanks, all the articles I've referenced provide semiempirical results for the parameters, but how can they differ that much from each other?

I mean, if the parameters at Table 4 were taken at T = 0 K, Delta_a very similar to the one provided in Datta's book, but Delta_c differs in one order of magnitude. Do you how what fenomena can occur in those measurements so that the results are so different?