ErwinZumer
- 1
- 1
Hi
Let's consider a potential of the form
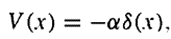
The Schrodinger equation reads
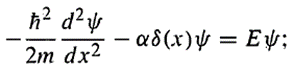
as shown in the book 'Introduction to Quantum mechanis' by D.J. Griffiths, Chaper 2 Section 5, the solution of the equation yields (only for bound state, which means E<0):
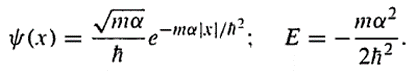
My question:
if i have one particle and i apply this potential on it, how does it take one value of energy?
another question is, if i have one paricle with some energy, E, before applying this potential, does the energy of the particle will change?
Let's consider a potential of the form
The Schrodinger equation reads
as shown in the book 'Introduction to Quantum mechanis' by D.J. Griffiths, Chaper 2 Section 5, the solution of the equation yields (only for bound state, which means E<0):
My question:
if i have one particle and i apply this potential on it, how does it take one value of energy?
another question is, if i have one paricle with some energy, E, before applying this potential, does the energy of the particle will change?