mrneglect
- 11
- 0
I've got an exam tomorrow, and this is one of the topics I can't get my head around. Any help would be much appreciated.

I've calculated that alpha=4.78x10^9. I understand that a Delta function is a periodic potential much like this one...
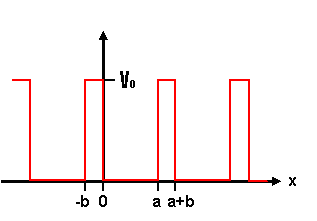
...EXCEPT that V0 --> infinity, b --> 0, but bV0 still has a finite area.
I can see that plotting the left-hand-side of the equation given in the question against (alpha x a) will result in this graph:
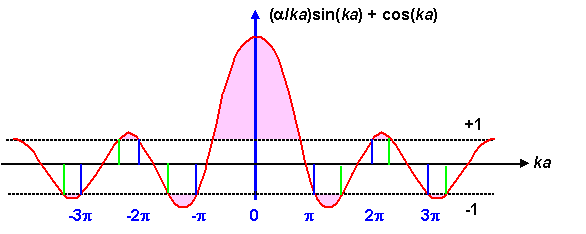
And I understand that for the equation to hold true, the left-hand-side cannot go above 1 or below -1, hence the regions shaded pink in the above plot are invalid solutions of the equation in the question.
I understand that what I am looking for is the energy band marked here:
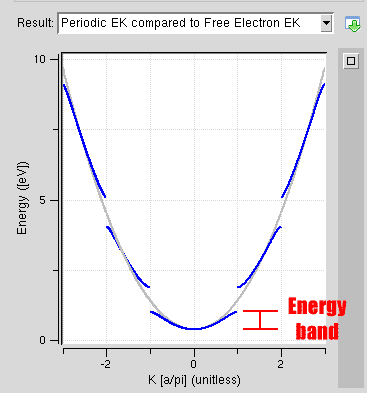
But I just don't know how to get it.
I understand what the question is asking, what the concepts mean, but I'm just lost in the mathematics.
As I said, any help would be greatly appreciated.
Cheers.
Homework Statement
Homework Equations
The Attempt at a Solution
I've calculated that alpha=4.78x10^9. I understand that a Delta function is a periodic potential much like this one...
...EXCEPT that V0 --> infinity, b --> 0, but bV0 still has a finite area.
I can see that plotting the left-hand-side of the equation given in the question against (alpha x a) will result in this graph:
And I understand that for the equation to hold true, the left-hand-side cannot go above 1 or below -1, hence the regions shaded pink in the above plot are invalid solutions of the equation in the question.
I understand that what I am looking for is the energy band marked here:
But I just don't know how to get it.
I understand what the question is asking, what the concepts mean, but I'm just lost in the mathematics.
As I said, any help would be greatly appreciated.
Cheers.
