- #1
Oliver321
- 59
- 5
Lets neglect conservation of momentum and assume that all frames of reference are inertial. Now imagine three objects: the sun, the Earth and an asteroid. In the inertial frame of the sun, Earth and asteroid are flying towards each other ( velocitys v and -v).
Now imagine you are standing at the surface of the earth: you see the asteroid flying towards you with 2v. So after some time the asteroid hits the Earth and all of its kinetic energy (K=2mv^2) gets converted into thermal energy (let’s assume the Earth stands still after the impact which implies that also the asteroid stands still). The temperature of the Earth rises.
Now look at this scenario from perspective of the sun:
Earth hast velocity -v and the asteroid has velocity v (so a velocity difference of 2v). They both hit each other. In the first moment the asteroid gets slowed down to zero (converting its kinetic energy in thermal energy) and in the exact same moment the asteroid gets accelerated to the velocity of the Earth (wich costs energy). But that would implie that really no kinetic energy gets converted into thermal energy, because the kinetic energy of the Earth and the asteroid are the same before and after the impact. Only the velocity of the asteroid points in the other direction. Nevertheless kinetic energy could not be negative so the direction plays no role.
Where is my mistake?
Thank you for your help!
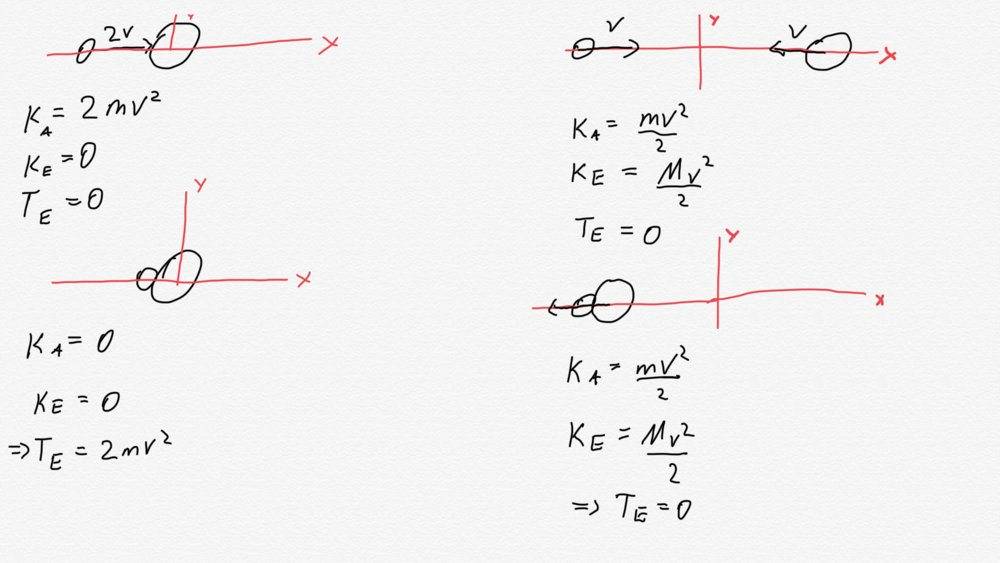
Now imagine you are standing at the surface of the earth: you see the asteroid flying towards you with 2v. So after some time the asteroid hits the Earth and all of its kinetic energy (K=2mv^2) gets converted into thermal energy (let’s assume the Earth stands still after the impact which implies that also the asteroid stands still). The temperature of the Earth rises.
Now look at this scenario from perspective of the sun:
Earth hast velocity -v and the asteroid has velocity v (so a velocity difference of 2v). They both hit each other. In the first moment the asteroid gets slowed down to zero (converting its kinetic energy in thermal energy) and in the exact same moment the asteroid gets accelerated to the velocity of the Earth (wich costs energy). But that would implie that really no kinetic energy gets converted into thermal energy, because the kinetic energy of the Earth and the asteroid are the same before and after the impact. Only the velocity of the asteroid points in the other direction. Nevertheless kinetic energy could not be negative so the direction plays no role.
Where is my mistake?
Thank you for your help!