- #1
George Zucas
- 47
- 0
EDIT: I accidentally put this thread into Engineering instead of Mechanical Engineering section, please move!
Hello all,
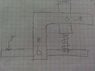
I am designing a system which will basically just stand in two different positions all the time by a compressed spring. The spring is pushing the system while the forces on the other side keep the system in place. There will be a sensor which will detect the time when the force is not there. This will work since when the force is not there, the spring will push the system up and the sensor will be triggered. Now I need to select a suitable spring.
I've approached the problem by calculating the potential energy change between the normal position and the position in which the sensor will be triggered ( IF there are any alternatives I'd be glad to learn it). It is about 10000 J (it is a small system). Now I need to find the energy lost to the bushings in the system (there are 8 bushings). The coefficient of friction is 0.19 and it is a H7-h9 fitting.
I am kinda at a loss to how to determine this. I don't know how the fitting comes into play for example or the roundness of the contact. What I would do is to take frictional force as F=mu*mg=0.19*0.25*9.81=0.47 N (0.25 is the shaft weight, 10 mm is radius) and therefore the frictional moment is 0.47*10=4.75Nmm. Though I don't where to go after that or how wrong it is up to this point.
Any help is appreciated.
Hello all,
I am designing a system which will basically just stand in two different positions all the time by a compressed spring. The spring is pushing the system while the forces on the other side keep the system in place. There will be a sensor which will detect the time when the force is not there. This will work since when the force is not there, the spring will push the system up and the sensor will be triggered. Now I need to select a suitable spring.
I've approached the problem by calculating the potential energy change between the normal position and the position in which the sensor will be triggered ( IF there are any alternatives I'd be glad to learn it). It is about 10000 J (it is a small system). Now I need to find the energy lost to the bushings in the system (there are 8 bushings). The coefficient of friction is 0.19 and it is a H7-h9 fitting.
I am kinda at a loss to how to determine this. I don't know how the fitting comes into play for example or the roundness of the contact. What I would do is to take frictional force as F=mu*mg=0.19*0.25*9.81=0.47 N (0.25 is the shaft weight, 10 mm is radius) and therefore the frictional moment is 0.47*10=4.75Nmm. Though I don't where to go after that or how wrong it is up to this point.
Any help is appreciated.
Last edited: