liuxinhua
- 79
- 1
During equal thickness interference, adjust the inclination of the two plates to expand the spacing of interference fringes to 10mm.
Then, if a light with a width of 5mm is used for equal thickness interference, whether an interference pattern will be observed, and the width of the interference pattern is less than the spacing of the interference fringes?
Move the light with a width of 5mm to present a bright fringe interference. The energy of the bright fringe will be greater than that of the light participating in the interference.
How can we reasonably explain this phenomenon?
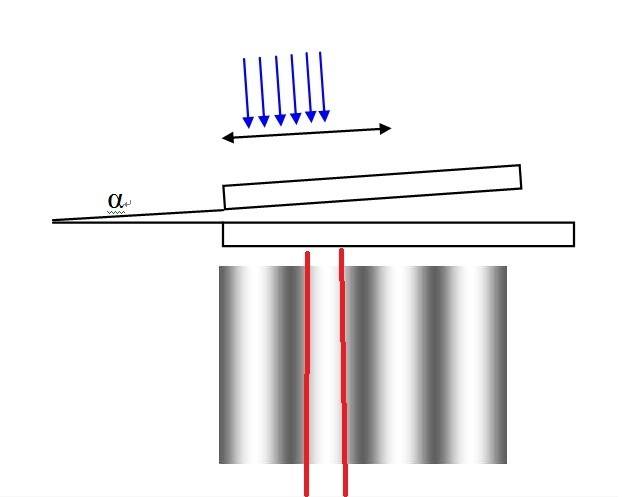
Then, if a light with a width of 5mm is used for equal thickness interference, whether an interference pattern will be observed, and the width of the interference pattern is less than the spacing of the interference fringes?
Move the light with a width of 5mm to present a bright fringe interference. The energy of the bright fringe will be greater than that of the light participating in the interference.
How can we reasonably explain this phenomenon?