- #1
Jason Louison
- 70
- 6
Hello Physics Forum Users! I have an annoying situation with the Finite Heat Release Equation used to simulate combustion and expansion processes in an internal combustion engine. The equation is as follows:
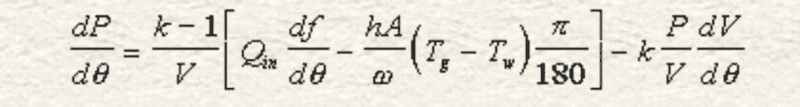
Nomenclature:
P = Cylinder Pressure (kPa)
θ = Crank Angle (Deg)
k = Specific Heat Ratio
V = Cylinder Volume (m3)
Qin = Heat Input (J)
ƒ = mass fraction burned (Wiebe Function, %)
h = heat transfer coefficient (W/m2-K)
A = Cylinder Wall Surface Area (m2)
ω = Engine Speed (rad/s..?)
Tg = Cylinder Gas Temperature (K)
Tw = Cylinder Wall Temperature (K)
I do not know why π/180 is there, maybe someone can explain it to me?
of course, df/dθ and dV/dθ are rate of change equations for Cylinder Volume and Mass Fraction Burned.
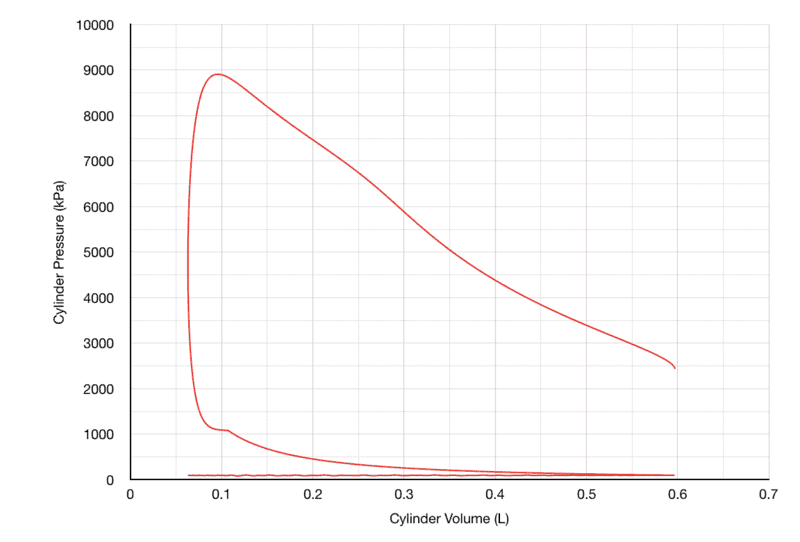
So, here's where things get a little weird. To obtain cylinder pressure, I Calculate dP/dθ, then multiply it by (1/720), and then add it to the initial pressure, p(θ-1). Yeah I know, it doesn't make much sense, in fact that right there may be my biggest mistake. But If I were to multiply dP/dθ by dθ, my data would be very inconclusive, as dθ for every cell is 1. multiplying the equation by 1 and adding it to the the initial pressure generates very weird data, and, unfortunately, some errors as well. The second issue is that when the engine speed is low, (Below 6500 RPM), The expansion pressure section is very obscure looking:
1000 RPM (Ignition Timing=-28° BTC): Way too much area under curve
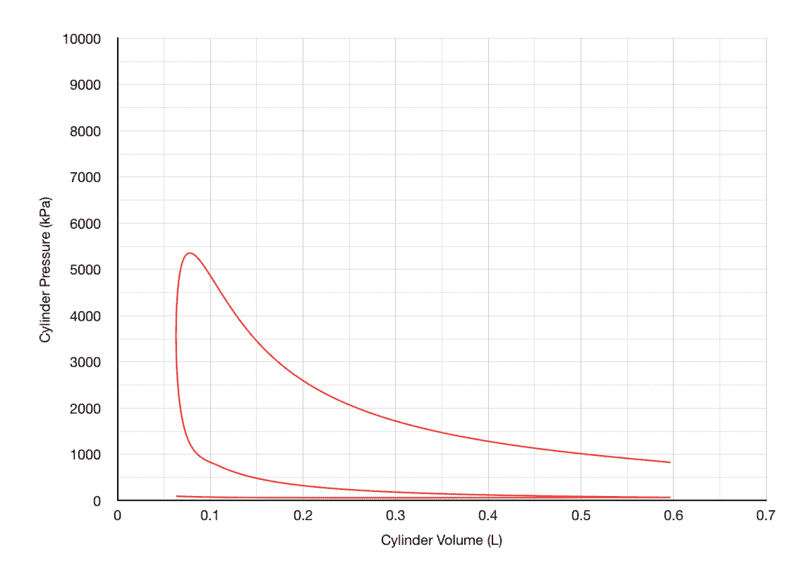
8500 RPM (Ignition Timing=-28° BTC): Normal-looking curve
Sources used:
https://www.engr.colostate.edu/~allan/engines.html
I have looked everywhere to try and find out what I am doing wrong, but I found nothing. :(
Nomenclature:
P = Cylinder Pressure (kPa)
θ = Crank Angle (Deg)
k = Specific Heat Ratio
V = Cylinder Volume (m3)
Qin = Heat Input (J)
ƒ = mass fraction burned (Wiebe Function, %)
h = heat transfer coefficient (W/m2-K)
A = Cylinder Wall Surface Area (m2)
ω = Engine Speed (rad/s..?)
Tg = Cylinder Gas Temperature (K)
Tw = Cylinder Wall Temperature (K)
I do not know why π/180 is there, maybe someone can explain it to me?
of course, df/dθ and dV/dθ are rate of change equations for Cylinder Volume and Mass Fraction Burned.
So, here's where things get a little weird. To obtain cylinder pressure, I Calculate dP/dθ, then multiply it by (1/720), and then add it to the initial pressure, p(θ-1). Yeah I know, it doesn't make much sense, in fact that right there may be my biggest mistake. But If I were to multiply dP/dθ by dθ, my data would be very inconclusive, as dθ for every cell is 1. multiplying the equation by 1 and adding it to the the initial pressure generates very weird data, and, unfortunately, some errors as well. The second issue is that when the engine speed is low, (Below 6500 RPM), The expansion pressure section is very obscure looking:
1000 RPM (Ignition Timing=-28° BTC): Way too much area under curve
8500 RPM (Ignition Timing=-28° BTC): Normal-looking curve
Sources used:
https://www.engr.colostate.edu/~allan/engines.html
I have looked everywhere to try and find out what I am doing wrong, but I found nothing. :(

