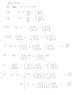- #1
nonequilibrium
- 1,439
- 2
In class my professor for thermodynamics made the following deduction:
We write [tex] dE = \left( \frac{dE}{dT} \right)_V dT + \left( \frac{dE}{dV} \right)_T dV[/tex]
And from the first law: [tex]dE = dQ - PdV[/tex] *
Equating and cancelling dE gives:
(1) [tex]dQ = \left( \frac{dE}{dT} \right)_V dT + \left( \left( \frac{dE}{dV} \right)_T + P \right) dV[/tex]
Realizing that [tex]\left( \frac{dE}{dT} \right)_V = C_V[/tex] and writing that [tex]dV = \left( \frac{dV}{dP} \right)_T dP + \left( \frac{dV}{dT} \right)_P dT[/tex]
We can fill this in in (1):
[tex]dQ = C_V dT + \left( \left( \frac{dE}{dV} \right)_T + P \right) \left( \left( \frac{dV}{dP} \right)_T dP + \left( \frac{dV}{dT} \right)_P dT \right)[/tex]
Now if we have an isobaric process (P = constant), then [tex]dP = 0[/tex], so then we can write:
[tex]dQ_P = C_V dT + \left( \left( \frac{dE}{dV} \right)_T + P \right) \left( \frac{dV}{dT} \right)_P dT[/tex]
Now "dividing both sides by dT" (mathematicians, be aware, I am playing with the ghosts of infinitesimals) and realizing that because dQ is isobaric: [tex]\frac{dQ}{dT} = \left( \frac{dH}{dT} \right)_P = C_P[/tex] we get:
[tex]C_P = C_V + \left( \left( \frac{dE}{dV} \right)_T + P \right) \left( \frac{dV}{dT} \right)_P[/tex]
Now, I'm assuming the relationship we got is correct?
But I'm wondering about the deduction... Is it truly valid?! (look at where I put the red star) Isn't dW = -PdV only true in a reversible change? Now someone might say "well, he actually meant to say dE = TdS - PdV and that is always valid" but then I say no, he cannot have meant that, because he also used that dQ = dH, so unless you want to imply dH = TdS for every process, this cannot be...
Now my point is not "can I find a completely different deduction that is surely correct" or "can the answer be correct", but really: what he did there, is that allowed? Cause if so, I'm not getting it.
Thank you,
mr. vodka
We write [tex] dE = \left( \frac{dE}{dT} \right)_V dT + \left( \frac{dE}{dV} \right)_T dV[/tex]
And from the first law: [tex]dE = dQ - PdV[/tex] *
Equating and cancelling dE gives:
(1) [tex]dQ = \left( \frac{dE}{dT} \right)_V dT + \left( \left( \frac{dE}{dV} \right)_T + P \right) dV[/tex]
Realizing that [tex]\left( \frac{dE}{dT} \right)_V = C_V[/tex] and writing that [tex]dV = \left( \frac{dV}{dP} \right)_T dP + \left( \frac{dV}{dT} \right)_P dT[/tex]
We can fill this in in (1):
[tex]dQ = C_V dT + \left( \left( \frac{dE}{dV} \right)_T + P \right) \left( \left( \frac{dV}{dP} \right)_T dP + \left( \frac{dV}{dT} \right)_P dT \right)[/tex]
Now if we have an isobaric process (P = constant), then [tex]dP = 0[/tex], so then we can write:
[tex]dQ_P = C_V dT + \left( \left( \frac{dE}{dV} \right)_T + P \right) \left( \frac{dV}{dT} \right)_P dT[/tex]
Now "dividing both sides by dT" (mathematicians, be aware, I am playing with the ghosts of infinitesimals) and realizing that because dQ is isobaric: [tex]\frac{dQ}{dT} = \left( \frac{dH}{dT} \right)_P = C_P[/tex] we get:
[tex]C_P = C_V + \left( \left( \frac{dE}{dV} \right)_T + P \right) \left( \frac{dV}{dT} \right)_P[/tex]
Now, I'm assuming the relationship we got is correct?
But I'm wondering about the deduction... Is it truly valid?! (look at where I put the red star) Isn't dW = -PdV only true in a reversible change? Now someone might say "well, he actually meant to say dE = TdS - PdV and that is always valid" but then I say no, he cannot have meant that, because he also used that dQ = dH, so unless you want to imply dH = TdS for every process, this cannot be...
Now my point is not "can I find a completely different deduction that is surely correct" or "can the answer be correct", but really: what he did there, is that allowed? Cause if so, I'm not getting it.
Thank you,
mr. vodka