Environmental Physics - Radiative forcing effect on greenhouse effect

[ProbablySid]

Homework Statement

To mitigate climate change, a large-scale afforestation project is commenced. The project aims to create a radiative forcing of $\Delta Q = -1.0 Wm^{-2}$ over 50 years by the removal of $CO_{2}$ through photosynthesis. Before the project is undertaken, a typical value of the outgoing longwave radiation (OLR) for the region is $160 Wm^{-2}$ and the average surface temperature is $292 K$. After complete afforestation (of 50 years), the OLR reduces to $145 Wm^{-2}$.

i) (a) Estimate the Greenhouse Effect, $G$, for the region before planting begins.
(b) The total feedback parameter, $\gamma$, for the region is found to be $2.1 Wm^{-2}K^{-1}$. Assuming that the forcing target associated with the afforestation earlier is met, estimate what the surface temperature change will be due to the plant growth, hence calculate $G$ for the region after afforestation.

Relevant Equations

$G=\sigma T^{4}_{s} - OLR$ where $T_{s}$ is the average surface temperature, $G$ is the Greenhouse Effect, and $OLR$ is the outgoing longwave radiation. $\sigma$ is the Stefan-Boltzmann Constant.

$\gamma = \frac{-Q_{ext}}{\Delta T_{s}}$ where $\gamma$ is the total climate feedback parameter, $Q_{ext}$ is the applied radiative forcing, and $\Delta T_{s}$ is the resulting change in temperature. I think this equation is relevant for (b).

I think part (a) is simple enough. Here is what I have done.
(a) $G=\sigma T^{4}_{s} - OLR$
$$ =\sigma (294)^{4} - 160 = 254 Wm^-{2} $$

Part (b) is where I am confused. I think I'm supposed to apply the second relevant equation, in order to get the change in average surface temperature due to the radiative forcing. Thus,

(b) $$\gamma = \frac{-Q_{ext}}{\Delta T_{s}} \longrightarrow 2.1 = -\frac{-1}{\Delta T_{s}} \longrightarrow \Delta T_{s} = +0.48 K$$
So now the temperature has increased from $292 K$ to $292.48 K$ as a result of the radiative forcing.
Thus,
$G = \sigma (294.48)^{4} - 145 = 272 Wm^{-2}$

but doesn't this imply afforestation has actually increased the Greenhouse effect? I would not expect this to be the case, which leads me to believe I may have done part (b) incorrectly. Any help/pointers would be greatly appreciated. This is my first time posting on this website, so I hope I have got the hang of the LaTeX. If it's easier to read, I've also attached an image of my working out.

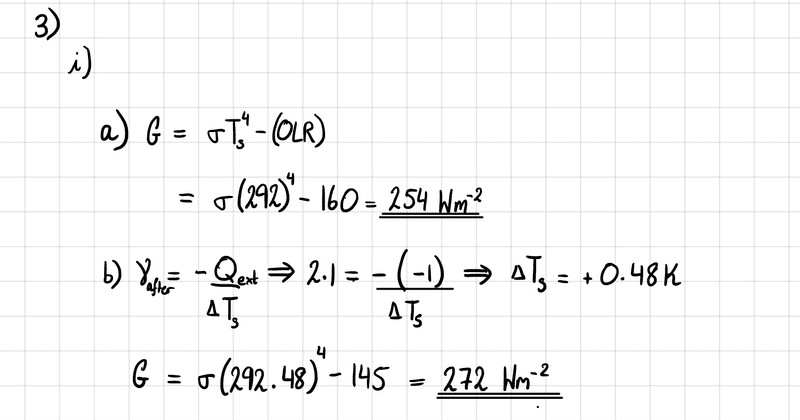Thank you very much.

 

[Steve4Physics]

Not familiar with this material but is it possible that the problem is simply due to confusion with names/sign-convention?

You have written:
$\Delta Q = -1.0 Wm^{-2}$ and
$\gamma = \frac{-Q_{ext}}{\Delta T_{s}}$
Then you treat $\Delta Q$ and $Q_{ext}$ as if they are the same thing.

But perhaps $Q_{ext}$ is intended to be a positive quantity here - so $Q_{ext} = -\Delta Q = 1.0 Wm^{-2}$.

Please note that's just an uninformed guess. If you check on your definitions of $\Delta Q$ and $Q_{ext}$ you should be able to tell.