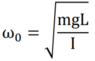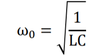- #1
Andrei0408
- 50
- 8
- Homework Statement
- I need the demonstration of the attached equations.
- Relevant Equations
- I've attached the 2 equations.
I've just learned about simple harmonic motion and I've been given the following examples: The physical pendulum (for small oscillations sin(theta)~theta), with the formula (1st pic), and the LC circuit, with the formula (2nd pic). If possible, I need the demonstration for these 2 formulas. Thank you!