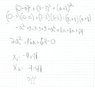Equation for a circle plugging for x and y, not getting a

[Femme_physics]

Homework Statement

http://img40.imageshack.us/img40/7174/thecircleu.jpg


A circle whose equation is


http://img830.imageshack.us/img830/5443/thecircle2.jpg


is tangent to the y-axis at point A(0,3) [see graph]. "a" is a parameter.

Find the value of a.

The Attempt at a Solution

Attached. I just plugged in A for x and y and solved. Where did I make a booboo?

 

[Mentallic]

You're making some errors in your working that need to be cleared up first.
You had $$(0-a)^2$$ to compute, and this should quickly be seen as $$(-a)^2=a^2$$ but instead you've gone through a longer route and forgot that $$(-a)(-a)=a^2$$ and not $$-a^2$$
Secondly, you expanded $$(3-3)^2=(3-3)(3-3)=9-9-9+9=0$$ You most definitely don't need to do all this work! Notice 3-3=0 so (3-3)²=0.

Once you clear up these problems, you should arrive at a correct answer.

 

[Femme_physics]

I'm going through the longer route because I don't have the mathematical insight you have. I need to compute things to actually see their result. My brain is not fused together with a calculator neuro-recepto-device like yours!

The fact that I automatically "need to know" what the result is doesn't give me a different answer, though. But regardless, without actually writing it down I can't tell. I'm not you.

 

[Mentallic]

Whether I have a neuro-recepto-device or not (does wolfram alpha count? ) it isn't needed to see things more clearly. You just need to understand what the math is telling you and get out of the habit of doing what you've done so many times before. You shouldn't look at a square of a sum and think "oh I need to expand because that's what I've done every other time", take a closer look at what you're doing.

(a+b)² means add a and b together, then square them. Another expression for this (without adding first then squaring) is a²+2ab+b². Now, both work because they're equivalent, but sometimes one is easier and more useful to use than another. For (3-3)², you don't want to be using the second expression to solve this, because 3-3 can be computed really easily!

edit:

Oh sorry I forgot to address this point

The fact that I automatically "need to know" what the result is doesn't give me a different answer, though.

It should give you a different answer because $$(0-a)^2=a^2$$ and you had $$-a^2$$

 

[Femme_physics]

But, should I really get a different result in the shorter way? It doesn't seem to matter how I go about expanding and simplifying the expression, it boils down to that which I've written in the 4th line

 

[Mentallic]

Your fourth line is $$-a^2=a^2+16a+64$$ and I'm telling you it's $$a^2=a^2+16a+64$$. Don't you see the difference? This one is very easy to solve, no quadratics

 

[Femme_physics]

Ah, I didn't switch the signs! *smacks forehead* I'm an idiot. Thanks :)

 

[Mentallic]

No worries