Equation for flux in reflected slab reactor

[StudioSaturn]

So, I've been at this for a while now. I am using my textbook (Introduction to NE, Lamarsh) and I cannot find a solution to calculate the thermal and fast fluxes in the reflector of a critical slab reactor. I have only been able to find solutions for the spherical shape, even online. As I understand it, the general solution is

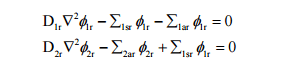
And for spherical geometry, the fast flux can be resolved in a finite reflector to be

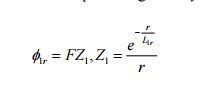
But what about the slab?
If anyone could point me to a source online, or if you could offer any help here it would be appreciated. I have been able to calculate the thermal and fast fluxes in the core, but the reflector has me stumped. Thanks in advance!

 

[StudioSaturn]

These are the equations I used for the core.
For thermal flux in the core:

And to get the fast flux from the thermal flux:

Also, I know that at the reflector-core interface, the fluxes must be continuous, and there is no neutron source term in the reflector. Thanks

 

[raining Pete]

Hi there,

I understand your frustration with not being able to find a solution for calculating thermal and fast fluxes in the reflector of a critical slab reactor. Have you tried looking at other textbooks or online resources? Sometimes different sources can offer different perspectives and approaches to solving problems.

One possible solution could be to use a numerical method such as Monte Carlo simulation to calculate the fluxes in the reflector. This method allows for more complex geometries and can be helpful in cases where analytical solutions are not readily available.

Another approach could be to simplify the slab geometry into a series of cylindrical shells and then use the cylindrical geometry solution to calculate the fluxes. This may not be an exact solution, but it could provide a good approximation.

I hope these suggestions help and good luck with your calculations!