Equation of motion: choice of generalized coordinates

[davidwinth]

TL;DR Summary

Why is it acceptable to choose an angle that doesn't coincide with a rotational arm?

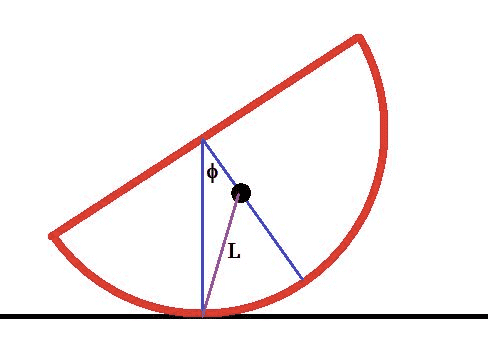
I am looking at a textbook solution to the following problem of finding the equation of motion of a half disk. In the solution, the author considers the half disk has a COM at the black dot, and to find the instantaneous translational velocity of the center of mass (he considers rotational velocity about the COM separately) the solution uses the angle phi and the fact that the instantaneous center of rotation is the point of contact with the ground at a distance L. Thus the velocity of the COM is given as:

V_c = L*d(phi)/dt

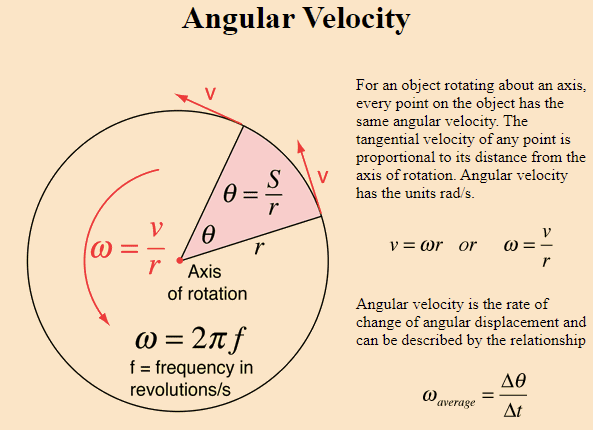
I understand that the differential velocity of a ball at the end of a string as it is swung is v = R d(phi)/dt where d(phi) is the angle the ball travels at a radius R during some moment of time, as shown in the second image. But the angle phi in the first image (the book solution) is NOT the angle through which the COM rotates about the contact point. How can the above expression for the velocity of the COM be correct?

 

[Vanadium 50]

That's the beauty of generalized coordinates. You can pick any ones you like. There aren't any right and wrong choices. (Well, there are some pathological wrong choices)

 

[davidwinth]

That's the beauty of generalized coordinates. You can pick any ones you like. There aren't any right and wrong choices. (Well, there are some pathological wrong choices)

Thank you for replying! I do agree with you about generalized coordinates and their usefulness. However, I think you missed the point.

My question is specifically about how it can be correct to describe the translational velocity of the center of mass by using an angle that is not the angle traversed about the instantaneous center of rotation. See the second image I provided, wherein the velocity of a mass is put in terms both of the angle it traverses about the center of rotation and the distance from the center of rotation during the traversal. The first image (the contended solution) has the distance from the center of rotation (so that seems correct) but uses a completely different angle. As far as I can see, the angles are not the same at all, nor is the chosen angle related in any meaningful way to the distance L. Is the implication that we could use any old angle/distance pair to come up with a correct equation of motion? Or is the distance L fixed, inexplicably, and only the angle can be any angle we come up with to pair the distance to? Either choice makes no physical sense when considering the way it is usually taught (i.e., again, the second image where the angle is the angle traversed about the center of rotation and the distance is the distance of the mass from the center of rotation during the traversal.)

I hope that clears up the issue. With the given choice of angle, I do not understand why that rotational distance "pairs" with it to produce a physically meaningful velocity when the angle formed between the ground, contact point, and center of mass would seem more in line with the way it is taught.

 

[Vanadium 50]

The technique lets you use any coordinates you like. (Of course, if they want the the answer in x and y and you write it in r and φ, it will be marked wrong). Usually some choice of variables makes things simpler than some other choice, but you ca`n do it any way you like. So questions like "can I" have an easy answer - "yes". In this techique, the question is more "should I?". Some choices of variables lead more quickly to solutions than others.

 

[PeroK]

I hope that clears up the issue. With the given choice of angle, I do not understand why that rotational distance "pairs" with it to produce a physically meaningful velocity when the angle formed between the ground, contact point, and center of mass would seem more in line with the way it is taught.

Did you check to see whether $V_c = L\frac{d\phi}{dt}$ is correct?

Note that $L$ is a function of $t$, so it's not immediately clear to me why you can write down the speed of the centre of mass as $L\frac{d\phi}{dt}$.

But, if you calculate $V_c$ directly, it turns out to be precisely this. Sometimes you have to roll your sleeves up and do some calculations.

 

[davidwinth]

Thanks everyone.

The consensus seems to be that picking any random angle "just works" for any problem, whether there is any physically interpretable reason apparent or not. So, one could use the angle the top surface makes with the ground, either of the other two angles in the triangle I drew, the angle formed by the ground, contact point and COM, the angle of the shadow cast by the sun, etc.

This is utterly mysterious! The thing that bothers me about this is that not all of these angles vary over the same range of values for a set range of physical motions, so that d(phi)/dt is not necessarily equal to d(theta)/dt for the sun-shadow angle. But then somehow, mysteriously, L*d(phi)/dt and L*d(theta)/dt both work?

If anyone reading this can come up with a physical explanation for this (not a "it just works" explanation), then I would love to hear it!

Thanks again.

 

[PeroK]

The consensus seems to be that picking any random angle "just works" for any problem, whether there is any physically interpretable reason apparent or not.

Eh?

So, one could use the angle the top surface makes with the ground, either of the other two angles in the triangle I drew, the angle formed by the ground, contact point and COM, the angle of the shadow cast by the sun, etc.

This is utterly mysterious! The thing that bothers me about this is that not all of these angles vary over the same range of values for a set range of physical motions, so that d(phi)/dt is not necessarily equal to d(theta)/dt for the sun-shadow angle. But then somehow, mysteriously, L*d(phi)/dt and L*d(theta)/dt both work?

If $V_c = L \frac{d\phi}{dt}$, then that doesn't hold for any angle other than $\phi$ (plus or minus a constant).

If anyone reading this can come up with a physical explanation for this (not a "it just works" explanation), then I would love to hear it!

Physics is about calculations, not mysticism!

 

[davidwinth]

Eh?

If $V_c = L \frac{d\phi}{dt}$, then that doesn't hold for any angle other than $\phi$ (plus or minus a constant).

Physics is about calculations, not mysticism!

I am not sure what you mean by, "Eh?" above. See the previous replies where I was told this technique lets you use "any coordinates you like" and similar. Your comment that L*d(phi)/dt will not work for any other angle (other than phi+C) contradicts what others have said. Mysticism is not any part of my comment. And while physics may be about calculation, it is not at all only about calculation. A good physicist will have a good physical intuition and insight into why things work, not just a facility with numerical manipulations.

EDITED TO ADD:
I am starting to think that they key to understanding why this works is that, for every choice of angle, the solution can only proceed once L is translated into an expression that is in terms of that angle. In this way, the product can be the same for many different angle choices without the time derivatives of different angles being the same. That may be what I have been missing in my own understanding: The solution will proceed only after L has been expressed in terms of constants (such as disk radius) and the chosen angle.

 

[PeroK]

Mysticism is not any part of my comment. And while physics may be about calculation, it is not at all only about calculation. A good physicist will have a good physical intuition and insight into why things work, not just a facility with numerical manipulations.

I'll take trigonometry and the differential calculus over platitudes any day!

EDITED TO ADD:
I am starting to think that they key to understanding why this works is that, for every choice of angle, the solution can only proceed once L is translated into an expression that is in terms of that angle. In this way, the product can be the same for many different angle choices without the time derivatives of different angles being the same. That may be what I have been missing in my own understanding: The solution will proceed only after L has been expressed in terms of constants (such as disk radius) and the chosen angle.

Let's see the calculations then!

 

[davidwinth]

I'll take trigonometry and the differential calculus over platitudes any day!

Platitudes? You must be having a rough day! If you haven't learned that physics is not merely math, then I definitely can't help you. Yet it is. I'm sorry you think the search for insight beyond number crunching is trite.

Let's see the calculations then!

Nobody else was required to provide calculations when claiming that any choice of angle would work, so I feel no need to do so either. I am simply assuming the consensus is correct (I know... a risky maneuver) and trying to understand how that could be so. Number crunching can come later when I have a plausible reason to think crunching numbers will get somewhere interesting.

 

[PeroK]

Number crunching can come later when I have a plausible reason to think crunching numbers will get somewhere interesting.

I apologise. I didn't realise you had such a fear of putting pen to paper and doing some calculations. You will have to start eventually though. You can't learn to play tennis if you're unwilling to pick up a racket and try to hit the ball!

If you haven't learn that physics is not merely math, then I definitely can't help you.

I'm not the one asking for help here!

 

[Vanadium 50]

We get a lot of questions of the form "show me how this works quantitatively without math". This seldom works out well.

If you are asking why the Lagranian metyhod works, it's probably faster and more efficient to read the relevant section in a classical mechanics text than to ask us to type one in so you can read it.

One thing you seem confused about. If I change the variables, I need to change them everywhere. For example, if $L=a^4 + a^2$, then $dL/da = 4a^3 + 2a$. If $b = a^2$, I cannot say "no b's in that, so $dL/db = 0$. I first need to replace the a's with b's and then take the derivative with respect to b. $dL/db = 2b+ 1$.

You will get different equations of motion in terms of a than in terms of b. As you should.

 

[davidwinth]

I apologise. I didn't realise you had such a fear of putting pen to paper and doing some calculations. You will have to start eventually though. You can't learn to play tennis if you're unwilling to pick up a racket and try to hit the ball!I'm not the one asking for help here!

And I apologize. I didn't realize we were on an elementary school playground, where we pretend that because someone has a particular thing in mind and is not interested in your approach, that he thus "has such a fear" of anything. What a jerk! Please refrain from ever "helping" me again.

I was asking for help on a very specific thing... help with a physically intuitive explanaton of why something works out. Your insistance that I do some calculations is asinine. At best some calculations would indicate that things work out for this particular situation - but I'd still be left wondering why. If you do not understand what I mean by a physically intuitive or motivated explanation of why something works the way it does, that's fine! But for you to pretend everyone must learn the same way, or that I am "afraid" of calculations, is beyond pompous. Again, please do not ever respond to anything I write again, as you were not helpful and don't seem interested to listen to what I am actually saying.

 

[davidwinth]

We get a lot of questions of the form "show me how this works quantitatively without math". This seldom works out well.

If you are asking why the Lagranian metyhod works, it's probably faster and more efficient to read the relevant section in a classical mechanics text than to ask us to type one in so you can read it.

One thing you seem confused about. If I change the variables, I need to change them everywhere. For example, if $L=a^4 + a^2$, then $dL/da = 4a^3 + 2a$. If $b = a^2$, I cannot say "no b's in that, so $dL/db = 0$. I first need to replace the a's with b's and then take the derivative with respect to b. $dL/db = 2b+ 1$.

You will get different equations of motion in terms of a than in terms of b. As you should.

Interesting tidbit. Of course, if you had bothered to read any of the above, you'd know that I am clearly not asking, "show me how this works quantitatively without math." You really think a physically intuitive explanation is the very same thing as a quantitative explanation? Wow. They are not the same thing. Also, I can tell by the way you phrased your opener that there is some kind of good old boys club around here. I am not interested.

And no, I am not asking how lagrangian mechanics works! Wow, again.Thanks for pointing out a possible error. In any case I think I have found the explanation I was looking for, posted above in a previous reply.

 

[Dale]

Thread temporarily closed for moderation.

OK, I am reopening the thread. The rude comments are buried too well among other stuff, so I am not editing any of the previous posts. Nobody is required to post from this point on, but if you choose to do so it needs to be respectfully.

@Vanadium 50 and @PeroK please write as though the OP is your direct manager. One of the business types who doesn't understand the technical stuff but still controls your pay raises. They are rather limited on the technical side but are making a good faith effort to understand it more.

@davidwinth please write as though the other participants are each one of your professors for a required class that you are struggling in. They are the kind of teacher that focus more on learning than on grades. Their lectures are terse but they are making a good faith effort to teach you the material.

If any of you cannot write in that manner then please just stop.

Re: intuition. Intuition is the result of experience. In physics you build intuition through the experience of doing calculations. Don't complain when you ask for intuition and you get a response to do calculations. That is how the people you have asked formed their intuition. They are not dismissing you, they are telling you how you can get what you asked for.