Mech_LS24
- 148
- 16
- Homework Statement
- The angular velocity of rod CD is at the moment shown in the figure 6 rad/s. A moment is applied at rod CD of M = 450 Nm. Determine the force in rod AB, the horizontal and vertical force at pin D and the angular acceleration in rod CD given at the moment shown in the figure. The block has a mass of 50 kg and his center of mass is at point G. Neglect the masses of the rods.
- Relevant Equations
- (ag)n = w^2 * r
(ag)t = alpha * r
Hello,
Given the statement a described above. To find the forces at point D I drawn a kinematic scheme and FBD of rod CD. But why am I allowed to ignore the mass of 50 kg, the forces at point B and point A? I know the are some rules about this, but I just can't remember them anymore.. The figure of the situation can be found below.
See my sketch with calculations:
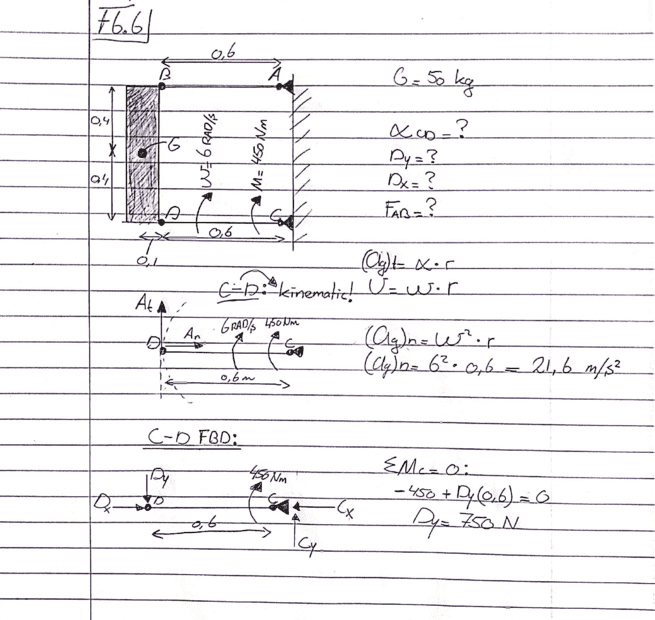
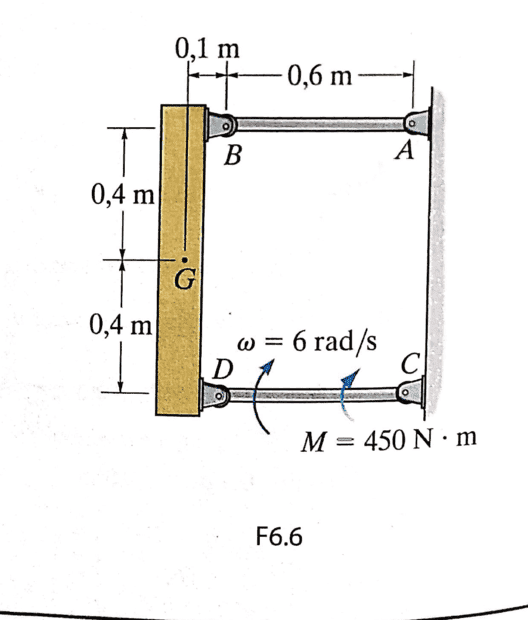
Given the statement a described above. To find the forces at point D I drawn a kinematic scheme and FBD of rod CD. But why am I allowed to ignore the mass of 50 kg, the forces at point B and point A? I know the are some rules about this, but I just can't remember them anymore.. The figure of the situation can be found below.
See my sketch with calculations:
 .
.