Equilateral triangle within a circumscribed circle

[Yankel]

Dear all,

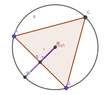
In the attached picture there is an equilateral triangle within a circumscribed circle.

MW is a radius of the circle, and I wish to prove that MT = TW, i.e., that the triangle cuts the radius into equal parts. I thought perhaps to draw lines AM and AW and to try and prove that I get two identical triangles, but failed to do so.

Can you kindly assist ?

Thank you !

View attachment 7682

 

[HallsofIvy]

Here's how I would do it. Call the radius of the circle "r". The three angles, AMB, AMC, and BMC are each 360/3= 120 degrees. The angle AMT is half that, 60 degrees. The right triangle AMT has hypotenuse of length r, angle at M 60 degrees so the length of MT is r cos(60)= r/2.

 

[Greg]

Is it given that $\overline{MW}$ is perpendicular to $\overline{AB}$?

 

[Yankel]

Greg, yes it is !

 

[Greg]

By the inscribed angle theorem $\angle{WAB}=\angle{WCB}=30^\circ$. It shouldn't be too difficult to finish up from there. :)

 

[MarkFL]

I would use coordinate geometry. Begin by orienting the circle such that its center is at the origin, and WLOG, give it a radius of 1 unit:

$$x^2+y^2=1$$

Now, the inscribed triangle has $\overline{AB}$ in quadrants I and IV as a vertical line. The line segment $\overline{MB}$ lines along:

$$y=\tan\left(60^{\circ}\right)x=\sqrt{3}x$$

Hence:

$$x^2+\left(\sqrt{3}x\right)^2=1$$

$$x^2=\frac{1}{4}$$

As $x$ must be positive, there results:

$$x=\frac{1}{2}$$

And so we conclude:

$$\overline{MT}=\overline{TW}$$