Equilibrium of Forces and Torques on Sawhorses Supporting a Person on a Board

[panda02]

Homework Statement

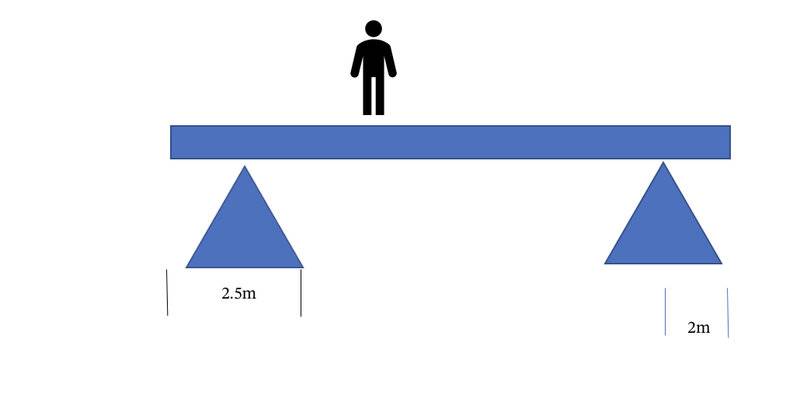
1. (20) If a uniform 20meter 400kg long board is placed on 2 sawhorses as shown in the picture and a 100kg Bill stands 6.5m from the left edge of the board. What are the forces on each sawhorse if the board doesn’t rotate?




2.5m
2m



b. What are the distances from your chosen pivot point to each object?


c. What are the Force equations?


d. What are the torque equations?



e. What are the forces of each sawhorse?

Relevant Equations

F1 + F2 = Fb
TorqueBill = Torqueboard

centre of mass of board at the centre of the board = at distance 6m from left end
At no rotation condition and equillibsium
IM= net moment of.
force = 0

If, = net horizontal force =-
ity = net vestical force =0
a. To prevent the board from rotating, the total torque on one side of the pivot point must be equal to the total torque on the other side.

b. Let's choose the left end of the board as our pivot point (point O).

c. The force equations:

For the sawhorse on the left (F1):
F1 - Weight of the board - Weight of Bill = 0 (no vertical acceleration)
F1 - 400 kg * 9.8 m/s² - 100 kg * 9.8 m/s² = 0
F1 - 3920 N - 980 N = 0
F1 = 3920 N + 980 N
F1 = 4900 N

For the sawhorse on the right (F2):
F2 - Weight of the board = 0 (no vertical acceleration)
F2 - 400 kg * 9.8 m/s² = 0
F2 - 3920 N = 0
F2 = 3920 N

d. The torque equations:

For Bill (standing 6.5 meters from the left end of the board):
Torque from Bill = Force × Distance
Torque_Bill = 100 kg * 9.8 m/s² * 6.5 m = 6370 N·m (clockwise torque)

For the board:
The board is uniform, so its weight acts at its center (10 meters from the left end). The torque from the board is zero at our chosen pivot point (O), as the perpendicular distance is zero.

e. The forces on each sawhorse:

Sawhorse on the left (F1) = 4900 N, directed upward.
Sawhorse on the right (F2) = 3920 N, directed upward.

The left sawhorse needs to support more weight because Bill is standing closer to it, creating a clockwise torque, and the right sawhorse supports less weight but still contributes to the equilibrium.

So, the forces on each sawhorse are 4900 N and 3920 N, respectively, directed upward.

It quite sure if I did this correctly
F2 = 4905
f1 0

 

[BvU]

Hello @panda02 ,

$\qquad$ !​

If you read back your post you can see it misses the picture. How far from the ends of the board are the sawhorse support points ?

Well, at least you got your post through the first step ...

$\$

 

[berkeman]

Can you post the picture that goes with the problem? Use the "Attach files" link below the Edit window to upload a PDF or JPEG image of the problem. Thanks.

 

[BvU]

a. To prevent the board from rotating, the total torque on one side of the pivot point must be equal to the total torque on the other side.

Torque doesn't have a side. Rephrasing: the torque on the board must be zero.

b. Let's choose the left end of the board as our pivot point (point O).

seems to conflict with

The torque from the board is zero at our chosen pivot point (O), as the perpendicular distance is zero

So here we have

The force balance is easy. It will have two unknowns (F1, F2)
now pick an axis of rotation and set up the torque expression. It will also have two unknowns.
Torque = 0 and force = 0 are two equations with 2 unknowns.

$\$

 

[Lnewqban]

Welcome, @panda02 !

Are you familiar with free body diagrams?
If not, please see:
https://courses.lumenlearning.com/s...apter/12-1-conditions-for-static-equilibrium/

 

[haruspex]

Let's choose the left end of the board as our pivot point (point O).

When there are unknown forces, it can help to pick an axis about which one or more of them has no torque.

 

[BvU]

When there are unknown forces, it can help to pick an axis about which one or more of them has no torque.

I fully agree, but it is worth noticing that $\Sigma$ torques = 0 for 'no rotation' holds for any choice.

$\$