Equilibrium of forces (angle of road so car will not skid)

[LuigiAM]

Hi everyone.

Our mechanics professor warned us that in the mid-term exam some students reached the right answer on some questions but their method was wrong. For this reason sometimes I'm worried when I reach the correct answer but the way I did it is different from the solution guide. And I don't want to just memorize solutions since if I just do that I'd be screwed in more advanced courses.

Here is one question where I'm a bit confused:

My solution is like this:

The forces acting on the car:
Normal force from the road = m g cosθ
Force down the slope = m g sin θ
Force up the slope = mv² / r

My sketch:

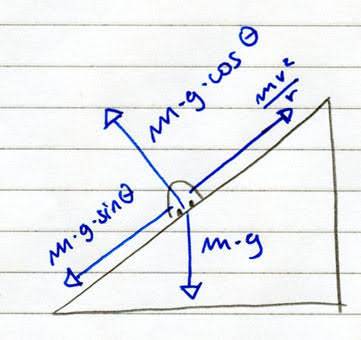
My solution:

The car does not skid, therefore the force down the slope and the force away from the slope must be equal (equilibrium of forces).

The force up the slope is equal to mv² / r since the highway is circular, and so it is the force away from the center of the circle (centrifugal force).

90 km/h * 1000m / 3600s = 25 m/s

m g sin θ = mv² / r
==> m on both side of equation cancel out:
g sin θ = v² / r

(9.8) sin θ = 25² / 500

(9.8) sin θ = 1.25

sin θ = 1.25 / 9.8 = 0.128

θ = arcsin(0.128) = 7.3 degrees

Is my method correct?

When I read the professor's solution it seems much more complicated. I didn't really understand his explanation when we did the problem in class (I'm hard of hearing and the professor is in his 80s and speaks very softly... not a good combination)

My understanding of the way the professor did it is that he placed mv² / r as the centripetal force straight toward the center of the circle (instead of at an angle like I did) but in the end he does have the same equation that I do with (9.8) sin θ = 25² / 500.

Also, I don't understand why he does Rn cos θ = m g. I think he's considering equilibrium of the forces in both directions instead of just one direction as I did?

Thanks for any help!

 

[Abhishek kumar]

First of all its not centrifugal force its centripetal force
look at your fbd it is wrong. How can you write mv^2/r=mgsinθ
Is these force are in same axis?

 

[kuruman]

Your method is incorrect because it is based on an incorrect free body diagram. It's OK, though unconventional, to draw it in the accelerating frame as you have. However,
1. The centrifugal force mv²/r should be directed away from the center of the horizontal circle that the mass describes. This would make it horizontal to the right.
2. You cannot assume that the normal force is N = mg cosθ. That's the case for a mass on an incline sliding up, down or at rest. Here, the presence of the centrifugal force changes its value to whatever is needed to have zero vertical acceleration. Yes, you need to apply Newton's Second Law in two dimensions.

 

[LuigiAM]

Thanks for the responses..

The professor wrote Rn cosθ in the solution, is this the same as m g cosθ?

As for the horizontal forces, is it wrong that it is mv² / r in one direction and mg sin θ in the other? Phew I'm really confused by this one :(

 

[Abhishek kumar]

Thanks for the responses..

The professor wrote Rn cosθ in the solution, is this the same as m g cosθ?

As for the horizontal forces, is it wrong that it is mv² / r in one direction and mg sin θ in the other? Phew I'm really confused by this one :(

Mg=Rncosθ
Rnsinθ is the force responsible to provide centripetal force to move car in circular banked

 

[kuruman]

It's a pity that the solved example does not provide a free body diagram. The correct FBD, in an inertial frame, should have only two forces on the block, the weight mg straight down as you have and the reaction force R_n perpendicular to the incline. In the accelerated frame that you use, you should add the centrifugal force mv²/r in the horizontal direction to the right. This results in 3 forces, the x and y components of which must separately add to zero. Do that and see what you get.

 

[LuigiAM]

Is this better?

 

[Abhishek kumar]

Is this better?

View attachment 216586

centrifugal force is pseudo force which is used when we work from rotating frame.Go through the book.

 

[kuruman]

Is this better?

You can work from this diagram, or you can follow @Abishek kumar's suggestion in which case the pseudo force should not appear in the diagram, but on the other side of the equation for the horizontal components as mass times acceleration. The difference between the two treatments is that in the inertial (non-accelerated) frame the sum of the horizontal forces is R_n sinθ which is set equal to mv²/r so that you get R_n sinθ = mv²/r. (Here we assume the positive direction to the left.) In the accelerated (non-inertial) frame the acceleration is zero, but there is a negative fictitious centrifugal force to the right. The sum of all the forces is zero because the acceleration is zero. Then you get the equation R_n sinθ - mv²/r = 0. This is the same equation as the previous one except that mv²/r has shifted to the left with a change of sign. The two approaches give you the same equation, so use whichever one makes you more comfortable.

 

[LuigiAM]

Thanks for the help!

If I understand the theory then, mv² / r is the magnitude of the centripetal force directed toward the center of the circle, but it is also the magnitude of the "fictional" centrifugal force that is directed away from the center. So it's basically a fictional reaction force that is derived using Newton's first law.

If I direct mv² / r toward the center of the circle, then it is the centripetal force. In this case, it is not a force that is added to the horizontal component of Rn but it actually IS the horizontal component of Rn. In this case, Rn_x is equal to mv² / r. This is algebraically equivalent to what happens if you use the fictional centrifugal force mv² / r.

Am I correct?

If I look carefully at the solution that the professor gave us, it seems that he put mv² / r to the left as a centripetal force then?

(phew, physics his hard, but I'm just coming back to "real" school after 15 years in law so be patient with me lol)

 

[kuruman]

You are almost there. Here is the theory:
Newton's Second Law says $\vec{F}_{net}=m\vec{a}$
This is a vector equation which means "two equations in one". The x-component of the vector on the left is the same as the x-component of the vector on the right. Likewise, the y-component of the vector on the left is the same as the y-component of the vector on the right. In other words,
$F_{net,x}=ma_x$ (1a)
$F_{net,y}=ma_y$ (1b)
We have to find four things, two on the left and two on the right. Let's start with the net force (left side) which is the sum of all the real forces acting on the object. Look at the drawing with the horizontal $mv^2/r$ erased because it's not a real force. We have (assuming that the positive direction is to the left)
$F_{net,x}=R_N\sin \theta$
$F_{net,y}=R_N\cos \theta -mg$
Now for the right side. We will do it in the inertial (non-accelerated) frame first. We note that the acceleration has a horizontal component towards the center (centripetal acceleration). Therefore $a_x=v^2/r$. The vertical component is zero because the car travels in a horizontal circle, $a_y=0$. Therefore the right sides are
$ma_x=mv^2/r$
$ma_y=0$
We now put the left and right sides together as shown in Equations (1a) and (1b) to get
$R_N\sin \theta=mv^2/r$
$R_N\cos \theta -mg=0$ $~\rightarrow~$ $R_N\cos \theta =mg$.
The rest is algebra as shown in the solution of the example.
In the accelerated frame, the vertical equation is the same, $R_N\cos \theta -mg=0$. The horizontal equation differs in that the right side is moved over to the left side with a change of sign, $R_N\sin \theta-mv^2/r=0$. This is interpreted to mean that, from the viewpoint of the driver who moves together with the car, the car's acceleration is zero while there is an additional horizontal force to the right that appears only if the car is turning to the left.

The result in both frames is the same, because the equations are the same.

I hope this clarifies how this is done. Incidentally, if you are wondering why your answer is close to the answer provided in the solution, it's because the correct answer is given by $\tan \theta = 1.25/9.8$ while you have $\sin \theta = 1.25/9.8$. For small angles, less than about 10^o as is the case here, $\tan \theta \approx \sin \theta$.

 

[LuigiAM]

Wow thanks for the explanation!

Can you fly to Montreal and replace my Electricity and Magnetism teacher this winter?

 

[kuruman]

Wow thanks for the explanation!

You're welcome. It's important to get the foundations right.

Can you fly to Montreal and replace my Electricity and Magnetism teacher this winter?

Sorry, no can do. I taught at the University of Vermont for many years and I know what the Montreal winters are like. That's why I escaped to Texas upon my retirement.

 

[Abhishek kumar]

You can work from this diagram, or you can follow @Abishek kumar's suggestion in which case the pseudo force should not appear in the diagram, but on the other side of the equation for the horizontal components as mass times acceleration. The difference between the two treatments is that in the inertial (non-accelerated) frame the sum of the horizontal forces is R_n sinθ which is set equal to mv²/r so that you get R_n sinθ = mv²/r. (Here we assume the positive direction to the left.) In the accelerated (non-inertial) frame the acceleration is zero, but there is a negative fictitious centrifugal force to the right. The sum of all the forces is zero because the acceleration is zero. Then you get the equation R_n sinθ - mv²/r = 0. This is the same equation as the previous one except that mv²/r has shifted to the left with a change of sign. The two approaches give you the same equation, so use whichever one makes you more comfortable.

I suggest to apply centripetal force because judging car's motion in car's frame is peculiar.car is circulating with inertial frame and if we easily work from inertial frame then why we should go for non inertial frame

 

[jbriggs444]

I suggest to apply centripetal force because judging car's motion in car's frame is peculiar.car is circulating with inertial frame and if we easily work from inertial frame then why we should go for non inertial frame

Because it makes it a static situation?

Personally, my intuition prefers dealing with a stationary car subject to a fixed trio of forces than a moving car under a varying acceleration due to one fixed and one varying force. Fewer things to worry about. Though it does come down to the same equation in the end.