vcsharp2003
- 913
- 179
- Homework Statement
- Question:
Equipotential surfaces associated with an electric dipole are
a) spheres centered on the dipole
b) cylinders with axes along the dipole moment.
c) planes parallel to the dipole moment.
d) planes perpendicular to the dipole moment.
e) None of the above
- Relevant Equations
- None
The answer is given as (a), but I think it's not correct based on the equipotential surfaces diagram given in our book for an electric dipole as below.
The red dashed lines, which are supposed to be the equipotential surfaces, are surely not representing a sphere centred at the dipole center. So, in my view, the correct answer is "(e) None of the above".
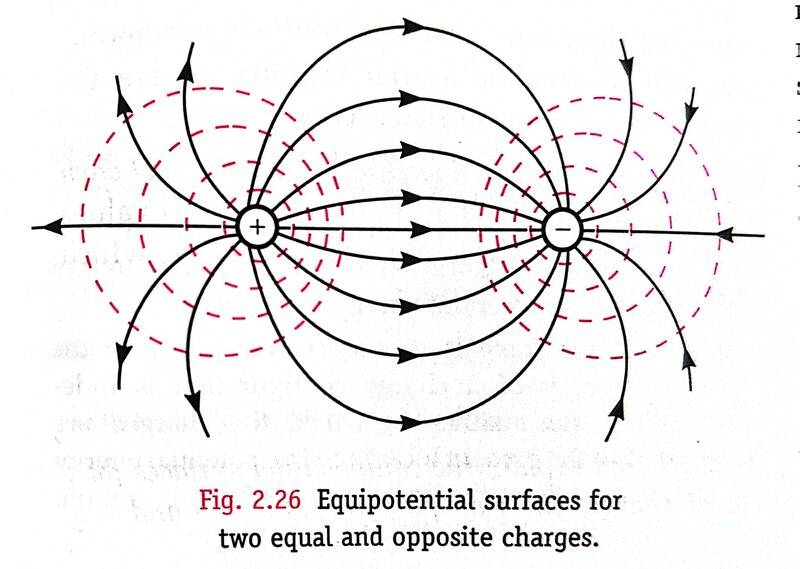
The red dashed lines, which are supposed to be the equipotential surfaces, are surely not representing a sphere centred at the dipole center. So, in my view, the correct answer is "(e) None of the above".
Last edited: