Portuga
- 56
- 6
- Homework Statement
- Prove that consider a Bravais lattice as in infinite array of discrete points with ann arrangemente and orientation that appears exactly the same, from whicever of the points the array is viewed, definition (a) from now on, implies that is can also be described as al points with position vectors ##\vec{R}=\sum_{i=1}^{3}n_{i}\vec{a}_{i}## where ##\vec a _ 1##, ##\vec a _ 2## and ##\vec a _ 3## are any three vectors not all in the same plane, and ##n_1##, ##n_2## and ##n_3## range throuhg all integral values.
- Relevant Equations
- No relevant equations for this one, only mathematical reasoning is necessary.
Proof. To demonstrate that a Bravais lattice (Figure 1) can be considered as a set of points located by a linear combination of primitive vectors of the lattice with integer coefficients, a sequence of claims in increasing order of complexity can be adopted. First, what is shown for one octant of Cartesian space will be valid for the others (hence only this octant is displayed in Figure 1, which does not affect the proof's development and facilitates diagram representation).
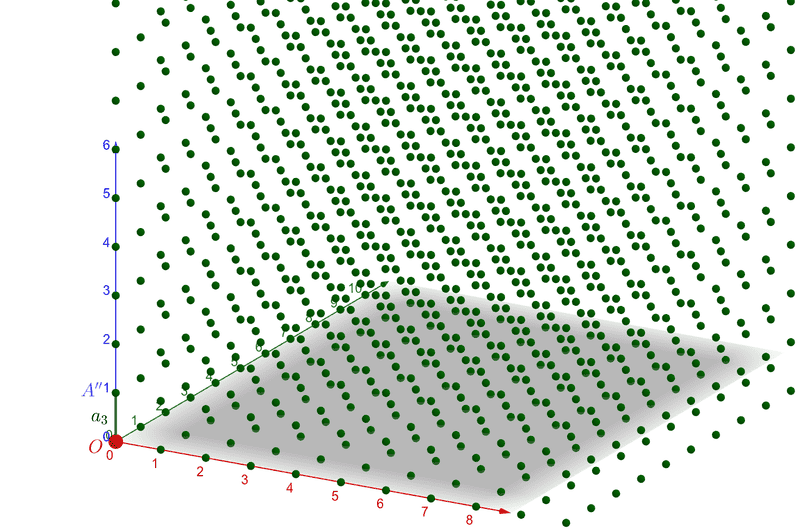
Figure 1.
Now, let's say an observer is at position O and looks towards position A. They will perceive it at a distance, let's say ##a_{1}## (Figure 2).

Figure 2.
By definition (a), this must also be the distance at which, being at A, they will perceive B (Figure 3).
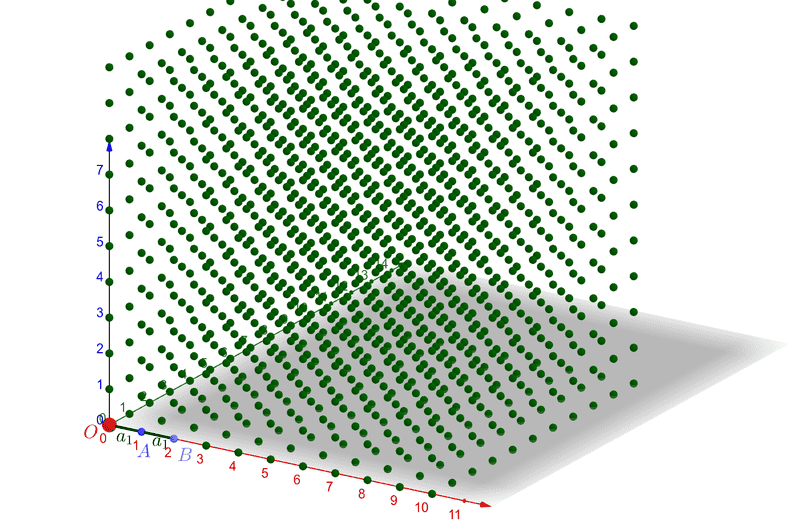
Figure 3.
For the same reason, any point in that direction from some other point will also be separated by ##a_{1}## from a neighbor thus chosen.
Consider again that the observer is at O, but this time looking towards position ##A^{\prime}## (Figure 4).
 Figure 4.
Figure 4.
If ##A^{\prime}## is separated by ##a_{2}## from O, by the previous argument, every neighbor adjacent to another in that direction will also be.
And if this time the observer looks towards position ##A^{\prime\prime}## and perceives a spacing of ##a_{3}##, by the arguments presented earlier, this will be the separation of any two adjacent neighbors in that direction.
Note that all neighbors are separated from their adjacent neighbors in the three alignment directions by distances ##a_{1}##, ##a_{2}##, and ##a_{3}##. Therefore, every position in the lattice is determined by a linear combination of integers of the vectors ##\vec{a}_{i}## whose magnitude is given by ##a_{i}##, and whose direction is the alignment between neighbors.
"So, any advice? Is this proof good, or is there still something I haven't noticed? Thank you."
Figure 1.
Now, let's say an observer is at position O and looks towards position A. They will perceive it at a distance, let's say ##a_{1}## (Figure 2).
Figure 2.
By definition (a), this must also be the distance at which, being at A, they will perceive B (Figure 3).
Figure 3.
For the same reason, any point in that direction from some other point will also be separated by ##a_{1}## from a neighbor thus chosen.
Consider again that the observer is at O, but this time looking towards position ##A^{\prime}## (Figure 4).
If ##A^{\prime}## is separated by ##a_{2}## from O, by the previous argument, every neighbor adjacent to another in that direction will also be.
And if this time the observer looks towards position ##A^{\prime\prime}## and perceives a spacing of ##a_{3}##, by the arguments presented earlier, this will be the separation of any two adjacent neighbors in that direction.
Note that all neighbors are separated from their adjacent neighbors in the three alignment directions by distances ##a_{1}##, ##a_{2}##, and ##a_{3}##. Therefore, every position in the lattice is determined by a linear combination of integers of the vectors ##\vec{a}_{i}## whose magnitude is given by ##a_{i}##, and whose direction is the alignment between neighbors.
"So, any advice? Is this proof good, or is there still something I haven't noticed? Thank you."