- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
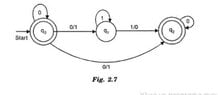
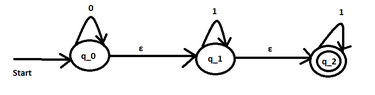
I am looking at the equivalence of NFAs with $\epsilon$-moves to NFAs without $\epsilon$-moves.
View attachment 5767
View attachment 5768
Why do we have to add a transition on $1$ from $q_0$ to $q_1$ although we don't have an arrow from $q_0$ to $q_1$ that corresponds to the symbol $1$?
I am looking at the equivalence of NFAs with $\epsilon$-moves to NFAs without $\epsilon$-moves.
View attachment 5767
View attachment 5768
Why do we have to add a transition on $1$ from $q_0$ to $q_1$ although we don't have an arrow from $q_0$ to $q_1$ that corresponds to the symbol $1$?