Equivalent capacitance of a circuit

[jolly_math]

Homework Statement

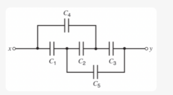
Find the equivalent capacitance between points x and y in the diagram below. Assume that C2 = 10 µF and that the other capacitors are all 4.0 µF.

Relevant Equations

in series: 1/C = 1/C1 + 1/C2
in parallel: C = C1 + C2

Why is it that, due to symmetry, ∆V2 = 0 and ∆V1 = ∆V4 = ∆V5 = ∆V3? I don't really understand the reasoning behind the simplification. Thank you.

 

[member 731016]

Is this how you worked the problem?

$C_1$ and $C_2$ are in series so we have an equivalent capacitor $C_{12}$

$C_{12}$ and $C_4$ are in parallel so we have an equivalent capacitor $C_{124}$

$C_3$ and $C_5$ are in parallel so we have an equivalent capacitor $C_{35}$

$C_{124}$ and $C_{35}$ are in series so we have an equivalent capacitor $C_{12345}$

 

[haruspex]

$C_1$ and $C_2$ are in series so we have an equivalent capacitor $C_{12}$

No, you can't do that. To be considered in series there must be no other circuit connection between the two.

 

[haruspex]

Why is it that, due to symmetry, ∆V2 = 0

It becomes obvious if you redraw the diagram. Remove 2 for the moment and draw the rest in a simple rectangle, then reinstate 2.

 

[member 731016]

No, you can't do that. To be considered in series there must be no other circuit connection between the two.

Whoops, sorry @haruspex thank you for picking up on that!

 

[member 731016]

It becomes obvious if you redraw the diagram. Remove 2 for the moment and draw the rest in a simple rectangle, then reinstate 2.

Thank you for your reply @haruspex !

I know my diagram is probably drawn incorrectly,

What are my mistakes thought?

Many thanks!

 

[jolly_math]

Why is it that, due to symmetry, ∆V2 = 0? If I remove V2, C1 and C4 (in parallel) are in series to C3 and C5 (in parallel). When I redraw V2, how I would be able to determine that V2 = 0? Thank you.

 

[SammyS]

Thank you for your reply @haruspex !

I know my diagram is probably drawn incorrectly,
View attachment 322555
What are my mistakes thought?

Many thanks!

Completely incorrect.

@haruspex was replying to OP, who at least realizes that ∆V₂ = 0 .

Added in Edit:
I had misread OP's question.

OP does not understand the symmetry argument justifying $\Delta V_2=0$ .

 

[scottdave]

Your circuit can be redrawn to look like this bridge circuit. That should help you understand.
https://en.m.wikipedia.org/wiki/Wheatstone_bridge

 

[member 731016]

Completely incorrect.

@haruspex was replying to OP, who at least realizes that ∆V₂ = 0 .

Thank you for your reply @SammyS!

Do you please know why ∆V2 = 0?

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex !

I know my diagram is probably drawn incorrectly,
View attachment 322555
What are my mistakes thought?

Many thanks!

Take it in steps. First, remove C₂, then straighten the rest of them diagram into a simple rectangle with two capacitors in series in the top line and the other two in the bottom.
Post those two.

 

[member 731016]

Take it in steps. First, remove C₂, then straighten the rest of them diagram into a simple rectangle with two capacitors in series in the top line and the other two in the bottom.
Post those two.

Thank you for your reply @haruspex !

Sorry for the late reply. I will do that.

Many thanks!

 

[member 731016]

Take it in steps. First, remove C₂, then straighten the rest of them diagram into a simple rectangle with two capacitors in series in the top line and the other two in the bottom.
Post those two.

Thank you for your reply @haruspex !

Here it is:

Step 1:

Step 2:

Many thanks!

 

[SammyS]

Thank you for your reply @haruspex !

Here it is:

Step 1:
View attachment 322619
Step 2:
View attachment 322620

Many thanks!

Not correct.

In the upper branch, you should have $C_4$ in series with $C_3$.

In the lower branch, you should have $C_1$ in series with $C_5$.

 

[member 731016]

Not correct.

In the upper branch, you should have $C_4$ in series with $C_3$.

In the lower branch, you should have $C_1$ in series with $C_5$.

Thank you for your reply @SammyS !

I think I see why they are not parallel now. It is because there along the wire there is another wire that splits off so not all the electrons join together again.

Here is my new diagram:

I think I see why the volage difference is zero now. Since capacitor two will cross between the two parallel branch's at either before or after the parallel capacitors as shown below: (I'm not sure whether you can tell where $C_2$ connects between the two branch's - Do you please know?)

So since $C_{43}$ is in parallel with $C_{12}$ then their potential difference across each will be the same. Therefore, they will read the same potential at the same distance down each wire.

Correct?

Many thanks!

 

[SammyS]

Thank you for your reply @SammyS !

I think I see why they are not parallel now. It is because there along the wire there is another wire that splits off so not all the electrons join together again.

Here is my new diagram:

Correct?

Many thanks!

Do not connect the series pairs. Make a drawing with the four capacitors as @haruspex and I suggested.

Then consider how/where to connect $C_2$ .

 

[member 731016]

Do not connect the series pairs. Make a drawing with the four capacitors as @haruspex and I suggested.

Then consider how/where to connect $C_2$ .

Thank you for your reply @SammyS!

Sorry for my mistake!

Here are the new diagrams,

And I think we connect $C_2$ here:

Many thanks!

 

[haruspex]

Thank you for your reply @SammyS!

Sorry for my mistake!

Here are the new diagrams,
View attachment 322627
And I think we connect $C_2$ here:
View attachment 322628

Many thanks!

Right. Do you see how the symmetry proves there is no potential across C2?

 

[member 731016]

Right. Do you see how the symmetry proves there is no potential across C2?

Thank you for your reply @haruspex !

Yes I think so, as along as the wires joining C2 to the circuit are perpendicular to the capacitors in series on each side then C2 and its wires will be equidistant from x so each side for the capacitor have the same potential and therefore have a zero potential difference

Many thanks!

 

[scottdave]

Thank you for your reply @haruspex !

Yes I think so, as along as the wires joining C2 to the circuit are perpendicular to the capacitors in series on each side then C2 and its wires will be equidistant from x. . . .

Depending on what frequencies you are working with, the geometry and distances of components can be an important factor.

 

[member 731016]

Depending on what frequencies you are working with, the geometry and distances of components can be an important factor.

Thank you @scottdave !

 

[SammyS]

Depending on what frequencies you are working with, the geometry and distances of components can be an important factor.

I think this questions in this thread are being asked at a very basic level.

 

[SammyS]

Thank you for your reply @haruspex !

Yes I think so, as along as the wires joining C2 to the circuit are perpendicular to the capacitors in series on each side then C2 and its wires will be equidistant from x so each side for the capacitor have the same potential and therefore have a zero potential difference

Many thanks!

If you mean that the wires are physically perpendicular, that has nothing to do with this situation.

The circuit, as modified by you, is electrically equivalent to the circuit given in the OP.

 

[member 731016]

If you mean that the wires are physically perpendicular, that has nothing to do with this situation.

The circuit, as modified by you, is electrically equivalent to the circuit given in the OP.

Thank you for your help @SammyS !

 

[scottdave]

I think this questions in this thread are being asked at a very basic level.

I thought so too - @Callumnc1 mentioned the wires are perpendicular and components equidistant, so I thought that I would mention it.

 

[member 731016]

I thought so too - @Callumnc1 mentioned the wires are perpendicular and components equidistant, so I thought that I would mention it.

Thank you for your reply @scottdave !