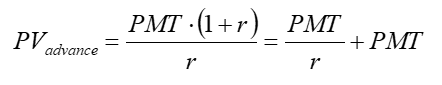logicandtruth
- 14
- 1
Hi all
I am currently working on questions focusing on valuation mathematics. A question on equivalent rates is perplexing me. The first question is straightforward, but I get stuck on the second question.
Q1. What is the value of the right to receive £100,000 annually in advance in perpetuity assuming a discount rate of 10%?
A1. £1,100,000
The formula below is for a level annuity that is received in perpetuity and in advance. Here in the UK typically commercial property leases are structured so tenants pay rents four times spread evenly over a year.
View attachment 8408
Q2. What is the value of the right to receive £100,000 per annum quarterly in advance in perpetuity assuming an annual nominal rate of 10%?
A. £1,062,344
I tried various iterations of the formula, but can't get the above answer. Any help would be much appreciated
I am currently working on questions focusing on valuation mathematics. A question on equivalent rates is perplexing me. The first question is straightforward, but I get stuck on the second question.
Q1. What is the value of the right to receive £100,000 annually in advance in perpetuity assuming a discount rate of 10%?
A1. £1,100,000
The formula below is for a level annuity that is received in perpetuity and in advance. Here in the UK typically commercial property leases are structured so tenants pay rents four times spread evenly over a year.
View attachment 8408
Q2. What is the value of the right to receive £100,000 per annum quarterly in advance in perpetuity assuming an annual nominal rate of 10%?
A. £1,062,344
I tried various iterations of the formula, but can't get the above answer. Any help would be much appreciated