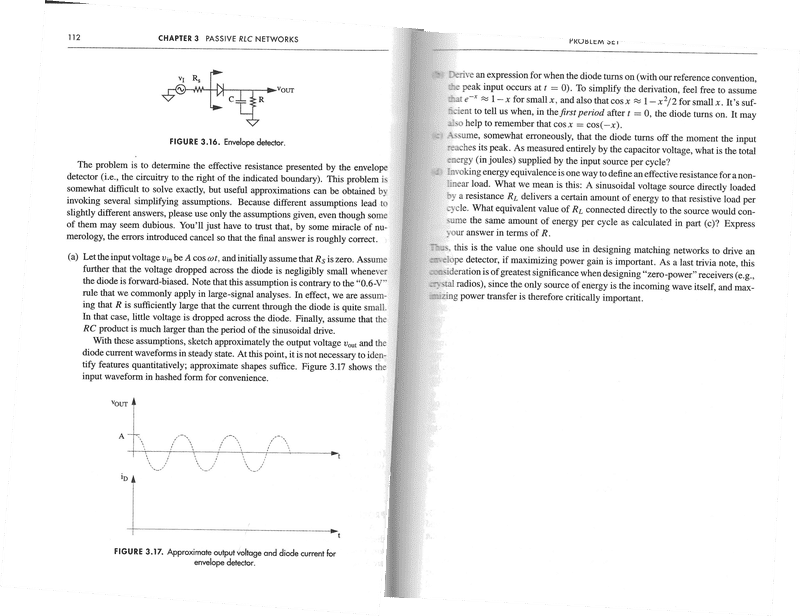
Jody
Gold Member
- 453
- 230
- Homework Statement
- (b) Derive an expression for when the diode turns on (with our reference convention, the peak input occurs at t=0). To simplify the derivation, feel free to assume that ##e^{-x} \approx 1-x## for small ##x##, and also that ##cos(x) \approx 1-x^2/2## for small ##x##.
(c) Assume, somewhat errorneously, that the diode turns off the moment the input reaches its peak. As measured entirely by the capacitor voltage, what is the total energy (in joules) supplied by the input source per cycle?
(d) Invoking energy equivalence is one way to define an effective resistance for a non-linear load. What we mean is this: A sinusoidal voltage source directly loaded by a resistance ##R_L## delivers a certain amount of energy to that resistive load per cycle. What equivalent value of ##R_L## connected directly to the source would consume the same amount of energy per cycle as calculated in part (c)? Express your answer in terms of ##R##.
- Relevant Equations
- (1) algebra, and (2) ##(1/2)CV^2##
Full problem:
I don't normally think about circuits like these in terms of energy (Joules) so I was very much confused.
What I did was find where the simplified expressions intercepts with each other to get the voltage. I scanned in my work although this text is a walk through of what I did. I used the simplified expressions were ##1-x## and ##1-t^2/2## although I shifted it by a period ##T##. The results is a quadratic and I chose the left side. This gives me what I think is ##t_{on}## for the diode, and I re-plug that into ##v(t)## which I'm assuming is ##A(1-x)## (I chose the left side because I think it would be easier). I set:
$$1-t = 1 - \frac{(t-T)^2}{2}$$
That leads to a quadratic assuming I can do algebra, which it depends on the day of the week so hopefully I'm posting this on a Wednesday
$$0 = t^2 - 2t(T+1) + T^2$$
Quadratic equation, and I chose the left side because it lands on the left side of that curve on ##T##
$$t = (T+1) - \sqrt{2T+1}$$
I plug that into ##v(t) = A(1-t)## line
$$v(t) = A(1 - [(T+1) - \sqrt{2T+1}]) = A(\sqrt{2T + 1} - T)$$
This part above is where I'm uncomfortable because it's all still black magic just math to me and I'm not feeling like I'm understanding earning something from that work. Then I'm thinking I need to enter it into ##E = (1/2)CV^2## an equation that's not from this book but I've seen it before, and the professor has agreed with me when I suggested it to him; however: This becomes really nasty and non-sensible at least in its current form. I go with it anyways and get the energy difference I call ##\Delta E##.
$$\Delta E = (1/2)C(V_1^2 - V_2^2) = (1/2)C(A^2 - A^2(1 - [(T+1) - \sqrt{2T+1}]) = A(\sqrt{2T + 1} - T)^2)$$
$$\Delta E = (1/2)CA^2 (1 - (\sqrt{2T+1} - T)^2)$$
I'm thinking... okay the units should be in Joules and I know that power is usually in Watts, which is the same as Joules per second. Maybe I could convert this back into the a sinusoid using the simplification and then use the same ##R## as a sinusoidal, but the form doesn't fit too well. If I try just ##V^2## it looks like it's going to turn into a bunch of non-meaningful garbage with some square root of the period. I'm pretty stumped at how to take my work and turn it into ##R_L## and how to include ##R##... not even sure if I'm on the right path.
edit: erm more thoughts about converting it back to cosine doesn't make sense because it would be constant :( I'm a bit baffled at that next step or how to make the conversion. I suppose I could just do the Joules over time if I got it right, but not sure how to get that ##R## in there.
My work:
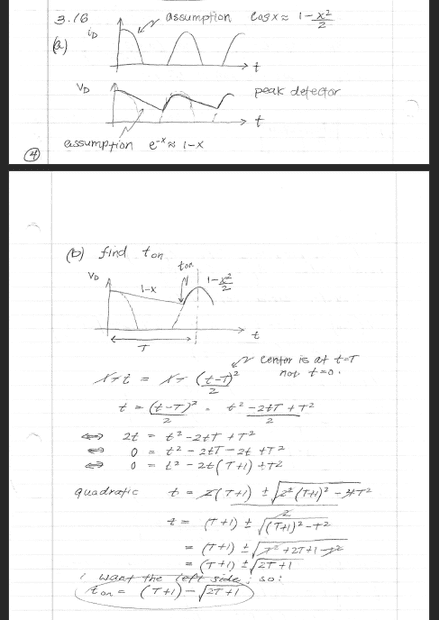

edit:
Professor posted his solutions. I'll share the strategy for future readers. Hrm for me this was really unintuitive I'm kind of surprised at how far I even got haha.
His strategy was to call ##v(t) = Ae^{-t/RC} \approx A(1-t/RC)## for that downward slope on the left side and then the right side parabolic one ##A(1-0.5(\omega t - 2\pi)^2)## (this one is from the small angle cosine simplification). He then set those two equal and solved for the quadratic for ##t##.
The part that I scribbled out in my work was on the right track ##\Delta E = 0.5CA^2 - 0.5C(A(1-t/RC))^2## he assumes that ##t/RC## is a really small number you can neglect.
The conversion to resistance ##\Delta E = V_{rms}^2 T / R## (just solved for ##\Delta E## in the previous step and so you can rearrange it for ##R##.
I don't normally think about circuits like these in terms of energy (Joules) so I was very much confused.
What I did was find where the simplified expressions intercepts with each other to get the voltage. I scanned in my work although this text is a walk through of what I did. I used the simplified expressions were ##1-x## and ##1-t^2/2## although I shifted it by a period ##T##. The results is a quadratic and I chose the left side. This gives me what I think is ##t_{on}## for the diode, and I re-plug that into ##v(t)## which I'm assuming is ##A(1-x)## (I chose the left side because I think it would be easier). I set:
$$1-t = 1 - \frac{(t-T)^2}{2}$$
That leads to a quadratic assuming I can do algebra, which it depends on the day of the week so hopefully I'm posting this on a Wednesday
$$0 = t^2 - 2t(T+1) + T^2$$
Quadratic equation, and I chose the left side because it lands on the left side of that curve on ##T##
$$t = (T+1) - \sqrt{2T+1}$$
I plug that into ##v(t) = A(1-t)## line
$$v(t) = A(1 - [(T+1) - \sqrt{2T+1}]) = A(\sqrt{2T + 1} - T)$$
This part above is where I'm uncomfortable because it's all still black magic just math to me and I'm not feeling like I'm understanding earning something from that work. Then I'm thinking I need to enter it into ##E = (1/2)CV^2## an equation that's not from this book but I've seen it before, and the professor has agreed with me when I suggested it to him; however: This becomes really nasty and non-sensible at least in its current form. I go with it anyways and get the energy difference I call ##\Delta E##.
$$\Delta E = (1/2)C(V_1^2 - V_2^2) = (1/2)C(A^2 - A^2(1 - [(T+1) - \sqrt{2T+1}]) = A(\sqrt{2T + 1} - T)^2)$$
$$\Delta E = (1/2)CA^2 (1 - (\sqrt{2T+1} - T)^2)$$
I'm thinking... okay the units should be in Joules and I know that power is usually in Watts, which is the same as Joules per second. Maybe I could convert this back into the a sinusoid using the simplification and then use the same ##R## as a sinusoidal, but the form doesn't fit too well. If I try just ##V^2## it looks like it's going to turn into a bunch of non-meaningful garbage with some square root of the period. I'm pretty stumped at how to take my work and turn it into ##R_L## and how to include ##R##... not even sure if I'm on the right path.
edit: erm more thoughts about converting it back to cosine doesn't make sense because it would be constant :( I'm a bit baffled at that next step or how to make the conversion. I suppose I could just do the Joules over time if I got it right, but not sure how to get that ##R## in there.
My work:
edit:
Professor posted his solutions. I'll share the strategy for future readers. Hrm for me this was really unintuitive I'm kind of surprised at how far I even got haha.
His strategy was to call ##v(t) = Ae^{-t/RC} \approx A(1-t/RC)## for that downward slope on the left side and then the right side parabolic one ##A(1-0.5(\omega t - 2\pi)^2)## (this one is from the small angle cosine simplification). He then set those two equal and solved for the quadratic for ##t##.
The part that I scribbled out in my work was on the right track ##\Delta E = 0.5CA^2 - 0.5C(A(1-t/RC))^2## he assumes that ##t/RC## is a really small number you can neglect.
The conversion to resistance ##\Delta E = V_{rms}^2 T / R## (just solved for ##\Delta E## in the previous step and so you can rearrange it for ##R##.
Last edited: