- 4,533
- 13
Problem:
Use importance sampling to estimate the quantity:
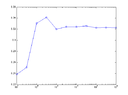
$$\theta = \int_{0}^{\infty}x \frac{e^{-(y-x)^2/2}e^{-3x}}{Z}dx$$, where $$Z=\int_{0}^{\infty}e^{-(y-x)^2/2}e^{-3x}dx$$ and $y=0.5$. Plot the converge of the estimator versus sample size. Note: You may consider $3e^{-3x}$ as the density for importance sampling.
Attempt:
This is a new topic that I digesting but as far as I understand it, this technique is used to reduce variance in Monte Carlo estimation and has a much faster convergence for small values. For example, if we want to estimate the $P[X>5]$ if $X$ is a standard normal random variable, then it will take a very large amount of samples to get this value so it's not practical.
If we are trying to estimate $$\theta=\int f(x)g(x)dx$$ we can rewrite this as $$\int \frac{f(x)g(x)}{h(x)}h(x)dx$$
This problem appears to take a similar form but I'm not sure what my first step is. According to my notes I should be trying find $\hat{\theta}$ by the following:
$$\hat{\theta}=\frac{1}{n} \sum_{i=1}^{n}\frac{f(X_i)g(X_i)}{h(X_i)}$$.
Can anyone provide some insight into the idea here or tips to get started?
Use importance sampling to estimate the quantity:
$$\theta = \int_{0}^{\infty}x \frac{e^{-(y-x)^2/2}e^{-3x}}{Z}dx$$, where $$Z=\int_{0}^{\infty}e^{-(y-x)^2/2}e^{-3x}dx$$ and $y=0.5$. Plot the converge of the estimator versus sample size. Note: You may consider $3e^{-3x}$ as the density for importance sampling.
Attempt:
This is a new topic that I digesting but as far as I understand it, this technique is used to reduce variance in Monte Carlo estimation and has a much faster convergence for small values. For example, if we want to estimate the $P[X>5]$ if $X$ is a standard normal random variable, then it will take a very large amount of samples to get this value so it's not practical.
If we are trying to estimate $$\theta=\int f(x)g(x)dx$$ we can rewrite this as $$\int \frac{f(x)g(x)}{h(x)}h(x)dx$$
This problem appears to take a similar form but I'm not sure what my first step is. According to my notes I should be trying find $\hat{\theta}$ by the following:
$$\hat{\theta}=\frac{1}{n} \sum_{i=1}^{n}\frac{f(X_i)g(X_i)}{h(X_i)}$$.
Can anyone provide some insight into the idea here or tips to get started?
Last edited: