Euler's method - geometrical explanation

[evinda]

Hello! (Wave)

We take into consideration the following ODE: $\left\{\begin{matrix}
y'=2t &, 0 \leq t \leq 1 \\
y(0)=0 &
\end{matrix}\right.$

Its solution is $y(t)=t^2$.

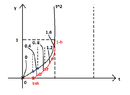
The following graph shows geometrically how Euler's method work.

View attachment 4063

$$y^{n+1}=y^n+hf(t^n,y^n)\\y^{n+1}=y^n+h \cdot 2 \cdot t^n$$

$$t^0=0, y^0 \ \ \ \ \ \ \ \ (t^0,y^0)$$We begin from $(t^0,y^0)=(0,0)$ and we draw the line that passes through $(t^0,y^0)$ and has slope $f(t^0,y^0)=0$.

We find the intersection point of this line with $t=t_1=h=0.2$.At the second step we begin from $(t^1,y^1)=(0.2,0)$ and we draw the line that passes from $(t^1,y^1)$ and has slope $f(t^1,y^1)=2t^1=2h=2 \cdot 0.2$.Could you explain further to me what we see from the graph? (Thinking)
I haven't really understood it... (Worried)

 

[jvicens]

Hello! (Wave)

Sure, I'd be happy to explain further. So, in this graph we can see how Euler's method works to approximate the solution to the given ODE. The blue line represents the exact solution, which we know is y = t^2. The red lines represent the successive approximations of the solution using Euler's method.

Starting from the initial point (t^0, y^0) = (0,0), we draw a line with slope f(t^0, y^0) = 0. This line represents the tangent to the exact solution at that point. Then, we find the intersection point of this line with t = t_1 = h = 0.2. This gives us the next approximation point (t^1, y^1).

For the second step, we use this new point as our starting point and draw a line with slope f(t^1, y^1) = 2t^1 = 2h = 2*0.2. This line represents the tangent to the exact solution at the new point, and we find the intersection point with t = t_2 = 2h = 0.4. This process continues, with each new line representing the tangent to the exact solution at the previous approximation point and finding the intersection with the next t value.

As we can see, the red lines get closer and closer to the blue line, which represents the exact solution. This is because Euler's method uses small steps to approximate the solution, and as we take more and more steps, the approximation becomes more accurate. I hope this helps to clarify things for you. (Smile)