guyvsdcsniper
- 264
- 37
- Homework Statement
- Cycle. A system undergoes the following four- stage cyclic process:
In stage (1) the system absorbs 226 cal of heat and does 50 J of work; in
(2) the system adiabatically does 30 J of work; and in (3) the system rejects
100 cal of heat while the environment does 80 J of work on the system.
Stage (4) is also adiabatic. Is work done on or by the system in stage (4)?
How many joules of work?
- Relevant Equations
- Q+W=0
Since this is a cycle, there should leave the system unchanged, hence Q+W = 0.
I wrote evaluated the heat and work done on/by the system at each cycle as shown in my work.
The first question ask is work done at the fourth stage. Since this a cycle and again the system she remain unchanged, and assuming the fourth stage is the last stage I can try to determine this by analyzing each cycle. The first stage absorbs 943.036J of heat. At the third stage, -418.6J of heat is expelled. That makes ΔQ = 527.436.
If the fourth stage is adiabatic, no heat can transfer at this stage. But since this is a cycle, the system must remain unchanged at the end. So that means there must be work done at the fourth stage in order to return back to the overall energy we started with.
We can say ΔQ=-W with W being each work done at each stage, -(W1+W2+W3+W4)
By algebra W4 = -527.436J.
So the system does work at this stage.
Is my approach correct?
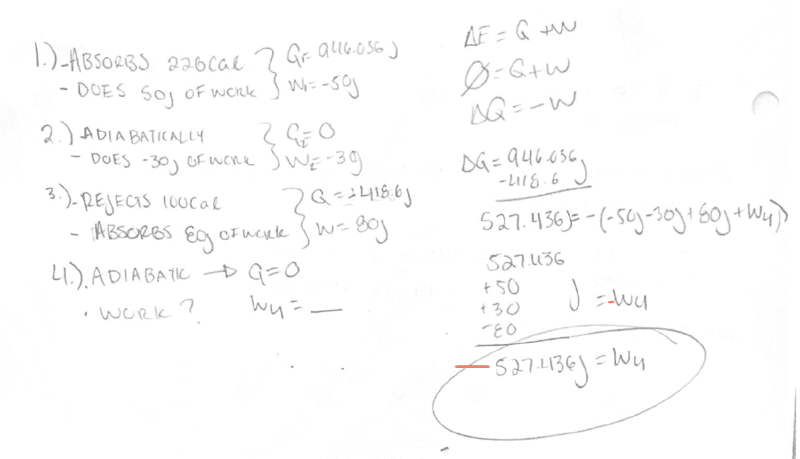
I wrote evaluated the heat and work done on/by the system at each cycle as shown in my work.
The first question ask is work done at the fourth stage. Since this a cycle and again the system she remain unchanged, and assuming the fourth stage is the last stage I can try to determine this by analyzing each cycle. The first stage absorbs 943.036J of heat. At the third stage, -418.6J of heat is expelled. That makes ΔQ = 527.436.
If the fourth stage is adiabatic, no heat can transfer at this stage. But since this is a cycle, the system must remain unchanged at the end. So that means there must be work done at the fourth stage in order to return back to the overall energy we started with.
We can say ΔQ=-W with W being each work done at each stage, -(W1+W2+W3+W4)
By algebra W4 = -527.436J.
So the system does work at this stage.
Is my approach correct?
