Evaluating a logarithmic integral using complex analysis

[Amad27]

Hello,

I am evaluating:

$$\int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} dx$$

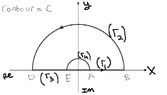
Using the following contour:

View attachment 3742

$R$ is the big radius, $\epsilon$ is small radius (of small circle)

Question before: Which $\log$ branch is this? I asked else they said,

$$-\pi/2 \le arg(z) \le 3\pi/2$$

But in the contour it is: $0 \le \theta \le \pi$ isn't it?

The pole is:

$z = \pm i$, but the one in the contour is $z = i$

$$\text{Res}_{z = i} = \lim_{z = i} \frac{\log^2(z)}{z+i} = \frac{\log^2(i)}{2i}$$

$$\log(z) = \log|z| + iarg(z) \implies \log(i) = \pi(i)/2 \implies \log^2(i) = -\frac{\pi^2}{4}$$

$$\text{Res}_{z = i} = \lim_{z = i} \frac{\log^2(z)}{z+i} = \frac{-\pi^2}{8i}$$

$$\oint_{C} f(z)dz = (2\pi i) \cdot \frac{\pi^2}{8i} = \frac{-\pi^3}{4}$$

Evaluation of $\Gamma_1$:

$$\oint_{\Gamma_1} f(z) dz = \int_{\epsilon}^{R} \frac{\log^2(x)}{x^2 + 1} dx$$

We will take $\epsilon \to 0$ and $R \to \infty$ later down the road.

Evaluation of $\Gamma_2$:

Using $z = Re^{i\theta}$ The denominator $z$'s are there for a reason.

$$\oint_{\Gamma_2} f(z) dz = \int_{0}^{\pi} \frac{\left( \log(R) + i\theta \right )^2 iRe^{i\theta} d\theta}{z)^2 + 1} $$

$$\left | \int_{0}^{\pi} \frac{\left( \log(R) + i\theta \right )^2 iRe^{i\theta} d\theta}{(Re^{i\theta})^2 + 1} \right | \le \int_{0}^{\pi} \frac{(R)\cdot \left | \log(R) + i\theta \right |^2}{\left | (z)^2 + 1 \right |} d\theta$$

$$|\log(R) + i\theta|^2 = \log^2(R) - \theta^2 \le \log^2(R)$$

$$|z^2 + 1| \ge |z|^2 - 1 \implies |z^2 + 1| \ge R^2 - 1$$

Then:

$$\frac{1}{|z^2 + 1|} \le \frac{1}{R^2 - 1}$$

The M-L inequality states:

$$\left | \int \right | \le ML(\Gamma)$$

Estimation lemma - Wikipedia, the free encyclopedia

So $M = \max(|f(z)|)$

$$|f(z)| \le \frac{\log^2(R)}{R^2 - 1}$$

$$L(\Gamma_2) = (1/2)(2\pi R) =\pi R $$

$$\left | \int \right | \le ML(\Gamma)$$

Therefore:

$$\left | \int \right | \le \frac{\log^2(R)\cdot\pi R}{R^2 - 1}$$

$$\lim_{R \to \infty} \left | \int f(z) dz \right | \le \lim_{R \to \infty} \int |f(z) dz| \le \lim_{R \to \infty} \frac{\log^2(R)\cdot\pi R}{R^2 - 1} = 0$$

So $\displaystyle \oint_{\Gamma_2} f(z) dz = 0$

Question: But how do I find the ACTUAL max $M$?? Was that the ABSOLUTE max? The absolute max is the criteria. Help?

Evaluation of $\Gamma_3$:

$$\oint_{\Gamma_3} f(z) dz = \int_{-R}^{-\epsilon} f(x) dx$$

Again, we will take limits, $\epsilon \to 0$ and $R \to \infty$ soon.

Evaluation of $\Gamma_4$:

$$\oint_{\Gamma_4} f(z) dz = \int_{\pi}^{0} \frac{\left( \log(\epsilon) + i\theta \right)^2 i\epsilon e^{i\theta}}{(\epsilon e^{i\theta})^2 + 1} d\theta$$

$$\left | \oint_{\Gamma_4} f(z) dz \right | \le \int_{0}^{\pi} \left | \frac{\left( \log(\epsilon) + i\theta \right)^2 i\epsilon e^{i\theta}}{(\epsilon e^{i\theta})^2 + 1} \right | d\theta $$

$$( \epsilon) \cdot \int_{0}^{\pi} \left | \frac{\left( \log(\epsilon) + i\theta \right)^2}{(\epsilon e^{i\theta})^2 + 1} \right | d\theta $$

$$\left | \left ( \log(\epsilon) + i\theta \right) \right |^2 = \log^2(\epsilon) - \theta^2 \le \log^2(\epsilon) $$

$$|z^2 + 1| \ge \epsilon^2 - 1$$

$$\therefore \frac{1}{|z^2 + 1|} \le \frac{1}{\epsilon^2 - 1}$$

$$|f(z)| \le \frac{\log^2(\epsilon)}{\epsilon^2 - 1} \le M$$

$$L(\Gamma_{4}) = (1/2)(2)(\pi \epsilon) = \pi \epsilon$$

$$\therefore ML(\Gamma) = \frac{\log^2{\epsilon}\pi\epsilon}{\epsilon^2 - 1}$$

$$\left | \oint f(z) dz \right | \le \int |f(z)| dz \le \frac{\log^2(\epsilon)\pi \epsilon}{\epsilon^2 - 1}$$

$$\lim_{epsilon \to 0} \left | \oint f(z) dz \right | \le \lim_{epsilon \to 0} \int |f(z)| dz \le \lim_{epsilon \to 0} \frac{\log^2(\epsilon)\pi \epsilon}{\epsilon^2 - 1}$$So:

$$\oint_{C} = \int_{\epsilon}^{R} \frac{\log^2(x)}{x^2 + 1} dx + \int_{0}^{\pi} \frac{\left( \log(R) + i\theta \right )^2 iRe^{i\theta} d\theta}{z)^2 + 1} + \int_{-R}^{-\epsilon} \frac{\log^2(x)}{x^2 + 1} dx + \int_{\pi}^{0} \frac{\left( \log(\epsilon) + i\theta \right)^2 i\epsilon e^{i\theta}}{(\epsilon e^{i\theta})^2 + 1} d\theta$$

$$\lim{R \to \infty}_{\epsilon \to 0} \oint_{C} = \int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} dx + \int_{0}^{\infty} \frac{\log^2(-x)}{x^2 + 1} dx = \frac{-\pi^3}{4}$$

Therefore,

$$ \int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} dx + \int_{0}^{\infty} \frac{\log^2(-x)}{x^2 + 1} dx = \frac{-\pi^3}{4}$$

Then we use $\log(z) = \log(|z|) + iarg(z)$ to get the required integral.

Can you just check the proofs for the integrals converging to $0$?

 

[chisigma]

The fact that the integral is negative should make you think that there must be something wrong somewhere... isn't it?... take into account that, solving the integral with the procedure illustrated in...

http://mathhelpboards.com/math-notes-49/integrals-natural-logarithm-5286.html

... the result should be...

$\displaystyle \int_{0}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}} \ d x = \int_{0}^{1} \frac{\ln ^{2} x}{1 + x^{2}} \ d x + \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x = \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x + \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x = $

$\displaystyle = 2\ \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x = 4\ \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2 k + 1)^{3}} = \frac{\pi ^{3}}{8}$

http://d16cgiik7nzsna.cloudfront.net/82/e7/i98953090._szw380h285_.jpgMerry Christmas from Serbia

$\chi$ $\sigma$

 

[alyafey22]

Evaluation of $\Gamma_3$:

$$\oint_{\Gamma_3} f(z) dz = \int_{-R}^{-\epsilon} f(x) dx$$

Does that imply that

$$\frac{\log^2(x)}{1+x^2} = \frac{\log^2(z)}{1+z^2}$$

On the negative x-axis ?

 

[Amad27]

The fact that the integral is negative should make you think that there must be something wrong somewhere... isn't it?... take into account that, solving the integral with the procedure illustrated in...

http://mathhelpboards.com/math-notes-49/integrals-natural-logarithm-5286.html

... the result should be...

$\displaystyle \int_{0}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}} \ d x = \int_{0}^{1} \frac{\ln ^{2} x}{1 + x^{2}} \ d x + \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x = \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x + \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x = $

$\displaystyle = 2\ \int_{1}^{\infty} \frac{\ln ^{2} x}{1 + x^{2}}\ d x = 4\ \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2 k + 1)^{3}} = \frac{\pi ^{3}}{8}$

Merry Christmas from Serbia

$\chi$ $\sigma$

$$I = \int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx + \int_{0}^{\infty} \frac{\log^2(-x)}{x^2 + 1} \,dx $$

$$\log(-x) = \log(x) + i\theta$$

Whatever theta is in $0 \le \theta \le \pi$$$I = \int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx + \int_{0}^{\infty} \frac{\left( \log(x) + i\theta \right)^2}{x^2 + 1} \,dx$$

$$I = \int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx + \int_{0}^{\infty} \frac{\log^2(x) + 2i\theta\log(x) - \theta^2}{x^2 + 1} \,dx$$

Because theta is $\pi$ for the negative x-axis and $0$ for positive x-axis.

$$I = 2\int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx + \int_{0}^{\infty} \frac{2i\pi\log(x) - \pi^2}{x^2 + 1} \,dx$$

$$I = 2\int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx + 0 - \pi^2 \int_{0}^{\infty} \frac{1}{x^2 + 1} dx = 2\int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx - (\pi^3)/2 = -\pi^3/4$$

$$2I = \frac{\pi^3}{4}$$

$$I = \frac{\pi^3}{8}$$

Now that that is done, I still need a way to prove:

$$\int_{0}^{\infty} \frac{2\pi\log(x)}{x^2 + 1} dx = 0$$

With complex analysis.

We could use the substitution $t = 1/x$ then prove that $-I = I$ which implies $I=0$ but that isn't rigorous at all. The goal is

Prove:

$$\int_{0}^{\infty} \frac{\log(x)}{x^2 + 1} dx = 0$$

I don't know, well, we'll see or we can always justify $x = 1/t$ so I suppose its fine.

Also, just a question,

How can we use contour integration with integrals from $0 \to 1$

My best guess would be to use the unit circle??

Thanks, and Merry Christmas from Turkmenistan.

@Zaid, it does imply the negative x-axis.

 

[alyafey22]

$$I = \int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} \,dx + \int_{0}^{\infty} \frac{\log^2(-x)}{x^2 + 1} \,dx $$

I would rewrite it as

$$\int_{-\infty}^0 \frac{(\ln |x|+i\pi)^2}{x^2+1}\,dx = \int_{0}^\infty \frac{(\ln (x)+i\pi)^2}{x^2+1}\,dx $$

For the other integral

$$I=\int^\infty_0 \frac{\log(x)}{x^2+1}\,dx$$

You can use the same method by integrating

$$f(z)= \frac{\log(z)}{1+z^2}$$

or , simply prove that $I=-I$.

 

[Amad27]

I would rewrite it as

$$\int_{-\infty}^0 \frac{(\ln |x|+i\pi)^2}{x^2+1}\,dx = \int_{0}^\infty \frac{(\ln (x)+i\pi)^2}{x^2+1}\,dx $$

For the other integral

$$I=\int^\infty_0 \frac{\log(x)}{x^2+1}\,dx$$

You can use the same method by integrating

$$f(z)= \frac{\log(z)}{1+z^2}$$

or , simply prove that $I=-I$.

It is actually very complicated from research, Ill work on it tomorrow and post updates.