- #1
- 683
- 412
- TL;DR Summary
- SymPy doesn't evaluate a sum
I want to evaluate the sum
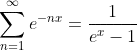
using Python and SymPy, I'm relatively new using SymPy and the first thing I tried was
But it doesn't work, it just returns the unevaluated sum. I can make it work using
But I would like to know if it is possible to make it work without need to break the expression into x^n and then substitute x by e^-x.
Thank you
using Python and SymPy, I'm relatively new using SymPy and the first thing I tried was
Python:
from sympy import exp, oo, summation, symbols
n, x = symbols('n,x')
summation(exp(-n*x), (n, 1, oo))But it doesn't work, it just returns the unevaluated sum. I can make it work using
Python:
from sympy import exp, oo, summation, symbols
n, x = symbols('n,x')
f = exp(-x)
summation(x**(-n), (n, 1, oo)).subs(x,f)But I would like to know if it is possible to make it work without need to break the expression into x^n and then substitute x by e^-x.
Thank you