Evaluation of integral having trigonometric functions

[WMDhamnekar]

Homework Statement

Evaluate $\displaystyle\iint\limits_R \sin{(\frac{x+y}{2})} \cos{(\frac{x-y}{2})}dA,$ where R is the triangle with vertices (0,0), (2,0) and (1,1).

Relevant Equations

Hint: Use the change of variables $u=\frac{x+y}{2}, v= \frac{x-y}{2}$

R is the triangle which area is enclosed by the line x=2, y=0 and y=x.
Let us try the substitution $u = \frac{x+y}{2}, v=\frac{x-y}{2}, \rightarrow x=2u-y , y= x-2v \rightarrow x= 2u-x + 2v \therefore x= u +v$
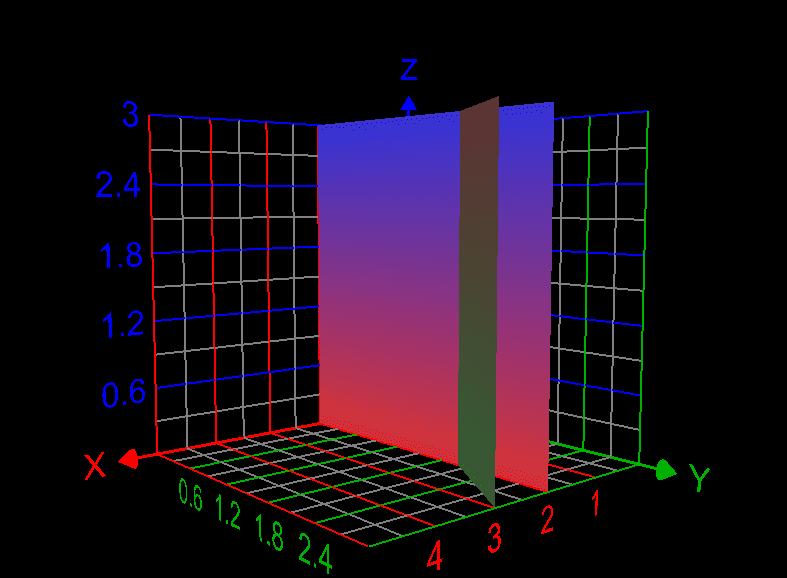
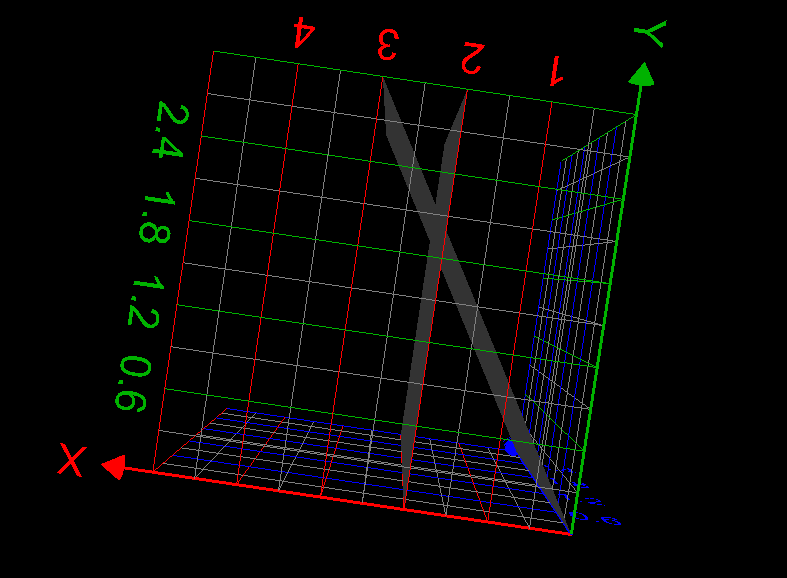
$y=x-2v \rightarrow y=2u-y-2v, \therefore y=u- v$ The sketch of triangle is as follows:

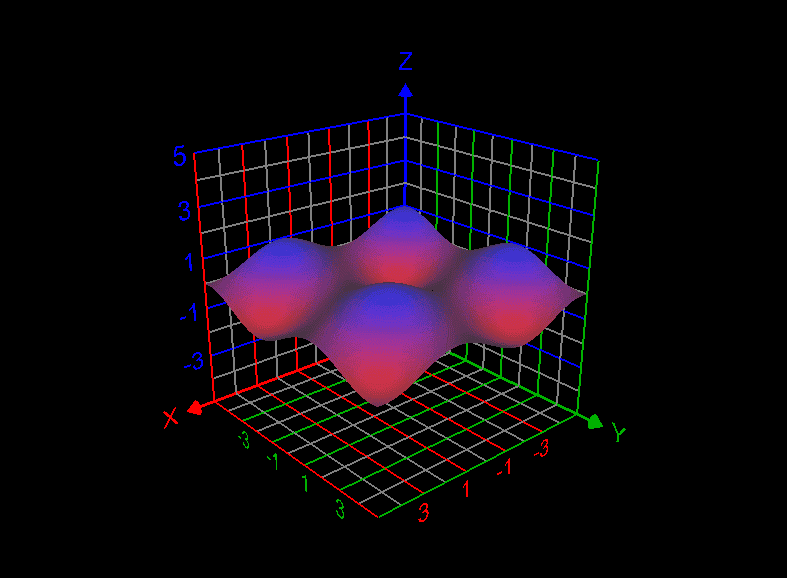
But when we plot sin((x + y)/2)*cos((x-y)/2), we get the below graph:

J(u,v)=|-2| = 2, So, now how to compute integration limits?

 

[WMDhamnekar]

I computed the answer as $\displaystyle\int_0^{0.5}\displaystyle\int_0^{1.5} 2*sin(u)*cos(v)du dv = 0.891024635191$ . But it is wrong. Correct answer provided is $1- \frac{sin(2)}{2} = 0.545351286587$

How is that? What is wrong with my answer?

 

[pasmith]

I computed the answer as $\displaystyle\int_0^{0.5}\displaystyle\int_0^{1.5} 2*sin(u)*cos(v)du dv = 0.891024635191$ . But it is wrong. Correct answer provided is $1- \frac{sin(2)}{2} = 0.545351286587$

How is that? What is wrong with my answer?

How did you arrive at those limits? You started with a triangle in the (x,y) plane. Does it seem sensible that you would end up with a rectangle in the (u,v) plane?

 

[WMDhamnekar]

How did you arrive at those limits? You started with a triangle in the (x,y) plane. Does it seem sensible that you would end up with a rectangle in the (u,v) plane?