Ex 0.2.5 in Sachs and Wu's textbook.

[MathematicalPhysicist]

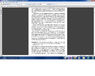
In the next attachements are:
1. Exercise 0.2.5 which I want help with.

2. Proposition 0.2.1 and its proof.

Now, basically a few things are changed in the theorem, I don't think I can use here the definition of s(t) in the proof of prop0.2.1 cause its s(t)=0, I don't think I can use this trick here.

Other thoughts that I had, obviously if I plug m=0 into prop0.2.1 I get that I should have:
$$\frac{d\gamma^1}{du}=\pm \frac{d\gamma^2}{du}$$, and $$\frac{d\gamma^2}{du}=a$$.

My question is how do I satisfy condition b in the theorem, I guess this x should be $$\pm Id +constant$$

 

[mark726]

Dear fellow scientist,

Thank you for sharing your thoughts and questions on this forum. I have reviewed the attachments and I believe I can offer some assistance with Exercise 0.2.5 and Proposition 0.2.1.

For Exercise 0.2.5, the key is to use the definition of s(t) given in the exercise, which is s(t) = 0. This means that s(t) is a constant function, and we can use this fact in our proof. One way to do this is to consider the derivative of s(t) with respect to t, which is 0. Then, using the chain rule, we can rewrite the condition given in the exercise as:

$$\frac{d\gamma^1}{du}=\frac{d\gamma^2}{du}\frac{ds}{dt}$$

Since s(t) is a constant, its derivative is 0, so the above equation simplifies to:

$$\frac{d\gamma^1}{du}=\frac{d\gamma^2}{du}(0)$$

We know that the derivative of s(t) is 0 because it is a constant function, and we can use this fact to simplify the condition in the exercise. I hope this helps with your understanding of Exercise 0.2.5.

Moving on to Proposition 0.2.1, you are correct in your thoughts about plugging in m=0 to get the equation:

$$\frac{d\gamma^1}{du}=\pm \frac{d\gamma^2}{du}$$

This is a valid approach and will help you satisfy condition b in the theorem. However, you also mentioned that x should be $$\pm Id +constant$$ to satisfy this condition. This is not necessarily true. The key is to find a solution for x that satisfies the equation:

$$\frac{d\gamma^1}{du}=\pm \frac{d\gamma^2}{du}$$

One approach is to let x be a constant function, such as x(u) = c, where c is a constant. Then, the derivative of x with respect to u is 0, and we can use this in our equation to satisfy condition b.

I hope this helps clarify things for you. If you have any further questions or need clarification, please do not hesitate to ask. Keep up the good work in your studies.