- #1
Freixas
- 307
- 42
I've searched high and low for an answer to my question and I can't find a thing.
Let's say I blow into the end of a tube. The opposite end is connected to a reed; when the air hits the reed, the reed vibrates and I can hear a sound. The harder I blow, the louder the reed sounds. I've tested this with a 15' tube while standing about 10' feet from the reed (the tube was partially coiled). The reed seems to respond immediately. If the pressure I create by blowing is transmitted down the tube at the speed of sound, then there is a 22ms latency in this system--that is, when I blow, the sound begins about 22ms later. If I blow less, the sound becomes quieter 22ms later.
Musicians can detect latencies of more than 12ms, but it varies by individual. Let's just say that I didn't notice any delays and so my test system suggests that the pressure changes at the starting end of the tube travel at close to (or faster than) the speed of sound.
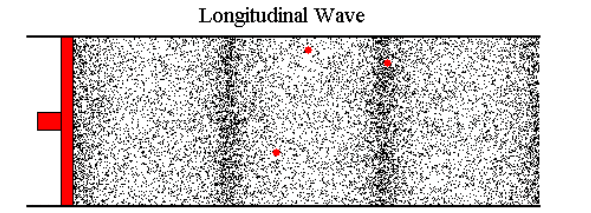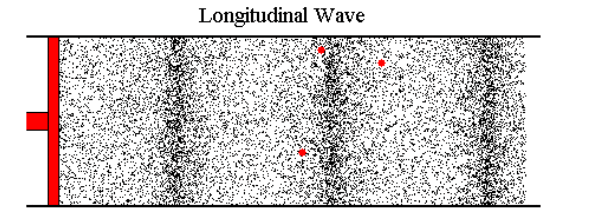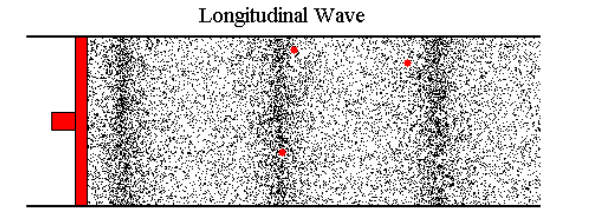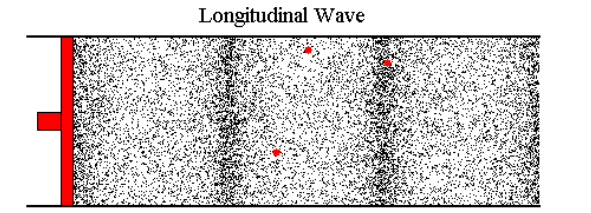
Most web pages that cover this topic usually start talking about sound, where the air molecules vibrate back and forth a tiny distance and, on average, don't go anywhere. But in the case I'm looking at, if I blow air in at 0.2 m/s, then air needs to flow out the other end at around 0.2 m/s (with perhaps a slight loss due to friction) and this velocity change (not just the wave front) has to travel down the tube at roughly the speed of sound (or faster).
Because it's hard to study the situation when things are changing continuously, let's imagine that we can immediately go from a flow of 0 m/s to 0.1 m/s. At the instant I start, the molecules of air in the tube are moving, on average, at 0 m/s. The are about to encounter an incoming wave of molecules whose average velocity is 0.1 m/s.
I've tried to picture what happens by using a billiard ball model, with billiard balls sitting on a perfectly flat, frictionless surface. I imagine a row of balls spaced out evenly and lined up perfectly (this is a one-dimensional model of a 3 dimensional problem). An incoming ball hits the first ball in the line and transfers all its kinetic energy to that ball. If the incoming ball is moving at 0.1 m/s, then after the collision its velocity is 0 and the ball it hit is now moving at 0.1 m/s and headed to the next ball in line.
The ball that stopped after the collision has many more balls coming toward it at 0.1 m/s, so it will get moving again. But the wave front (the collisions at the head of the line) doesn't appear to be moving any faster than 0.1 m/s. What needs to happen is
I'd be happy even with an explanation that showed how the wave front could move faster than the molecules flowing in without worrying about exactly how much faster this is. This still needs to explain how every molecule behind the wave front is moving at 0.1 m/s. In other words, the wave front, while moving (much) faster then 0.1 m/s, has to somehow speed up all the molecules it encounters to 0.1 m/s (on average).
Let's say I blow into the end of a tube. The opposite end is connected to a reed; when the air hits the reed, the reed vibrates and I can hear a sound. The harder I blow, the louder the reed sounds. I've tested this with a 15' tube while standing about 10' feet from the reed (the tube was partially coiled). The reed seems to respond immediately. If the pressure I create by blowing is transmitted down the tube at the speed of sound, then there is a 22ms latency in this system--that is, when I blow, the sound begins about 22ms later. If I blow less, the sound becomes quieter 22ms later.
Musicians can detect latencies of more than 12ms, but it varies by individual. Let's just say that I didn't notice any delays and so my test system suggests that the pressure changes at the starting end of the tube travel at close to (or faster than) the speed of sound.
Most web pages that cover this topic usually start talking about sound, where the air molecules vibrate back and forth a tiny distance and, on average, don't go anywhere. But in the case I'm looking at, if I blow air in at 0.2 m/s, then air needs to flow out the other end at around 0.2 m/s (with perhaps a slight loss due to friction) and this velocity change (not just the wave front) has to travel down the tube at roughly the speed of sound (or faster).
Because it's hard to study the situation when things are changing continuously, let's imagine that we can immediately go from a flow of 0 m/s to 0.1 m/s. At the instant I start, the molecules of air in the tube are moving, on average, at 0 m/s. The are about to encounter an incoming wave of molecules whose average velocity is 0.1 m/s.
I've tried to picture what happens by using a billiard ball model, with billiard balls sitting on a perfectly flat, frictionless surface. I imagine a row of balls spaced out evenly and lined up perfectly (this is a one-dimensional model of a 3 dimensional problem). An incoming ball hits the first ball in the line and transfers all its kinetic energy to that ball. If the incoming ball is moving at 0.1 m/s, then after the collision its velocity is 0 and the ball it hit is now moving at 0.1 m/s and headed to the next ball in line.
The ball that stopped after the collision has many more balls coming toward it at 0.1 m/s, so it will get moving again. But the wave front (the collisions at the head of the line) doesn't appear to be moving any faster than 0.1 m/s. What needs to happen is
- The wave front should be traveling faster than 0.1 m/s.
- Every molecule behind the wave front needs to be traveling 0.1 m/s.
I'd be happy even with an explanation that showed how the wave front could move faster than the molecules flowing in without worrying about exactly how much faster this is. This still needs to explain how every molecule behind the wave front is moving at 0.1 m/s. In other words, the wave front, while moving (much) faster then 0.1 m/s, has to somehow speed up all the molecules it encounters to 0.1 m/s (on average).